Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 2.17 - Ex. 13h
Em cada um dos exercícios determine a fórmula da função inversa. Fazer os gráficos da função dada e de sua inversa.
Passo 1
Galerinha, uma maneira rápida e prática de encontrarmos a função inversa de uma função é através da substituição das variáveis dessa função. Pode parecer confuso só falando assim, mas vamos ver na prática! Nessa questão queremos encontrar a inversa de . Então, para encontrarmos a inversa, primeiramente devemos trocar onde tem por e onde tem por . Assim,
O segundo passo é isolar o para encontrarmos nossa função inversa!
Passo 2
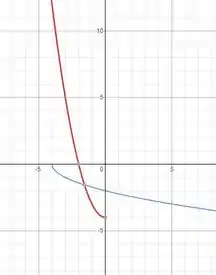
O gráfico a seguir apresenta essas duas funções! A função vermelha é a e a azul .
Resposta
A função inversa é
Exercícios de Livros Relacionados
Cada um dos exercícios 25-34 fornece uma fórmula para uma função y = f ( x ) . Em cada caso, determine f - 1 ( x ) e identifique o domínio e a imagem de f - 1 . Para conferir, mostre que f f - 1 x = f
Cada um dos exercícios 25-34 fornece uma fórmula para uma função y = f ( x ) . Em cada caso, determine f - 1 ( x ) e identifique o domínio e a imagem de f - 1 . Para conferir, mostre que f f - 1 x = f
Cada um dos exercícios 25-34 fornece uma fórmula para uma função y = f ( x ) . Em cada caso, determine f - 1 ( x ) e identifique o domínio e a imagem de f - 1 . Para conferir, mostre que f f - 1 x = f
Cada um dos exercícios 19-24 apresenta a fórmula de uma função y = f ( x ) e mostra os gráficos de f e f - 1 . Determine uma fórmula para f - 1 em cada caso.
Cada um dos Exercícios 11-16 apresenta o gráfico de uma função y = f ( x ) . Copie o gráfico e sobreponha-o à reta y = x . Em seguida, utilize a simetria com relação à reta y = x para adicionar o gráf