Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.5 - Ex. 17
17. Em cada parte, calcule a integral, sabendo que:
a)
b)
c)
d)
Passo 1
Vamos lá!! Vou primeiro desenhar o gráfico dessa função.
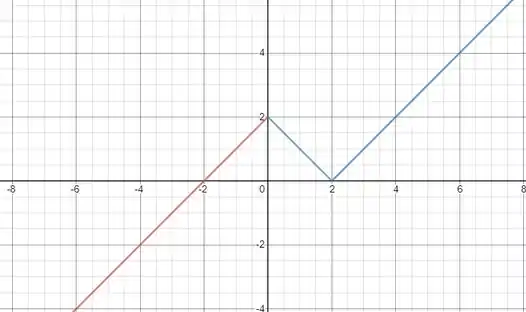
Sendo a parte em azul, a função .
E a parte vermelha, a função
Passo 2
Vamos para a letra a), precisamos achar a área que está em destaque, pois vamos de até .
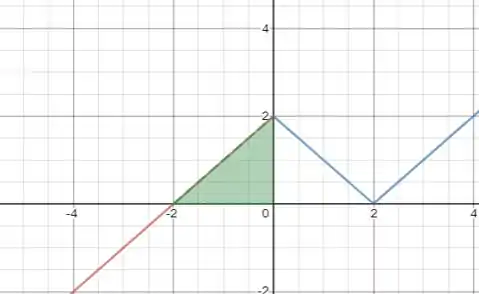
Temos que calcular a área desse triângulo retângulo, que é a multiplicação dos dois catetos.
O primeiro cateto vai de até , então tem comprimento igual a .
O segundo cateto vai de até , então tem comprimento igual a .
Como a integral é numericamente igual a área, temos:
Agora vamos para a letra b)
Temos que destacar a área que vai de a , então fica assim:
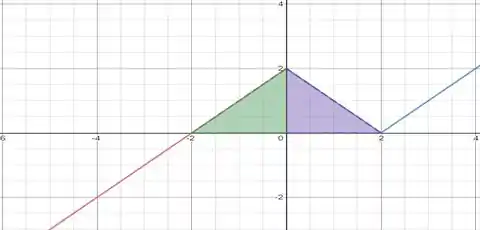
Sabemos a área do triângulo em verde, então só vamos calcular a área do triângulo em roxo e somar essas duas áreas:
Temos que calcular a área do triângulo retângulo em roxo, que é a multiplicação dos dois catetos.
O primeiro cateto vai de até , então tem comprimento igual a .
O segundo cateto vai de até , então tem comprimento igual a .
Como a integral é numericamente igual a área, e somando a área do triângulo em verde com a área do triângulo em roxo:
No passo 3, deixarei para fazer a c) e a d)
Passo 3
Vamos para a letra c)
A área destacada é de até , então é assim:
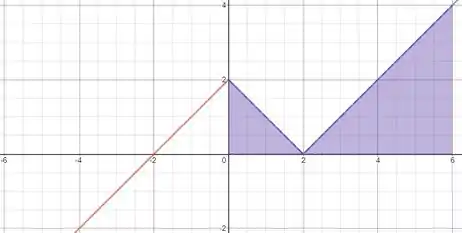
O triângulo menor já calculamos a área na letra b), essa área vale , então precisamos calcular a área do triângulo em roxo maior.
Temos que calcular a área do triângulo retângulo em roxo, que é a multiplicação dos dois catetos.
O primeiro cateto vai de até , então tem comprimento igual a .
O segundo cateto vai de até , então tem comprimento igual a .
Como a integral é numericamente igual a área, e somando a área do triângulo em roxo pequeno com a área do triângulo em roxo grande, temos:
Agora para terminarmos ufaaaa! Vamos para a letra d)
Na letra d), temos que o intervalo é de até , então destacando a área no gráfico, temos:
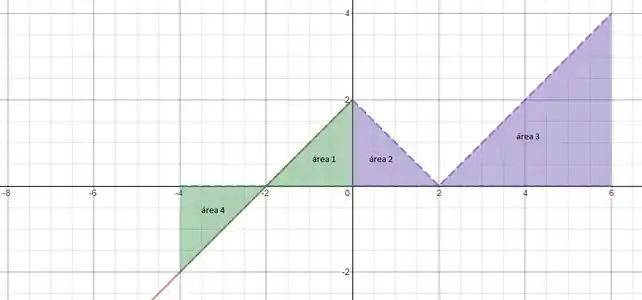
A área 1 nos já calculamos e o resultado é , então
Assim como a soma da área e a área 3, que é igual a , então
Só precisamos calcular a área , sabendo que quando a área da região 4 com sinal é negativa.
Vamos lá
Temos que calcular a área 4, que sendo um triângulo retângulo, é a multiplicação dos catetos.
O primeiro cateto vai de até , então tem comprimento igual a .
O segundo cateto vai de até , então tem comprimento igual a .
Porém essa área com sinal seria negativa, então temos que .
Como a integral é numericamente igual a área, vamos somar as áreas de todos esses triângulos, vamos lá!
Resposta
(a) 2
(b) 4
(c)
(d)