Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 6.11 - Ex. 19

int_0^(2 pi) | s e n x | d x

Passo 1

Nesse momento já temos o gráfico da função seno de cabeça certo??...Como não sei qual vai ser sua resposta vou botá-lo aqui de qualquer forma

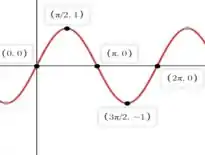
Ta vendo esse gráfico bonitinho ai em cima, GRAVA ELE, é muito importante!!!

Como estamos trabalhando com o módulo de senx significa que toda a parte que seria negativa da função vai ser rebatida para cima e ficar positiva.

Em questões desse tipo vamos sempre analisar a função em intervalos

Passo 2

f (x) = |s e n x| = {[[s e n x , 0 <= x <= pi],[- s e n x , pi < x <= 2 pi]])

Lembra da nossa regra..

int_b^a (f (x) + g ( x )) d x = int_b^a f ( x ) d x + int_b^a g ( x ) d x

Vamos utilizá-la aqui

int_0^(2 pi) | s e n x | d x = int_0^(pi) s e n x d x + int_(pi)^(2 pi) - s e n x d x

Mas sabemos que

int_0^(pi) s e n x d x = int_(pi)^(2 pi) - s e n x d x

Passo 3

Portanto

int_0^(2 pi) | s e n x | d x = 2 int_0^(pi) s e n x d x = 2 (- c o s x) (​|_0 -> pi = - 2 c o s pi + 2 c o s 0 = 4

Resposta

int_0^(2 pi) | s e n x | d x = 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calculeint_(- 1)^0 e^(- 2 x) d x
Calculeint_((1)/(2))^1 (s + 2) d s
Calculeint_0^((pi)/(3)) (3 + cos 3 x) d x
Calculeint_1^2 ((1 + 3 x^2)/(x)) d x
Calculeint_1^2 (1 - t^2)/(t^4) d t