Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 18a
Dê o domínio e esboce o gráfico.
Passo 1
Olá, tudo bem? Essa questão parece complicada, mas vou ajudar você!
Vamos começar multiplicando e dividindo pelo conjugado:
E simplificando o numerador temos:
Agora vamos pensar o seguinte: à medida que vai se tornando cada vez maior, o denominador da fração vai se tornando cada vez maior, e a fração vai se tornando cada vez mais próxima de zero.
Ou seja, à medida que cresce, a diferença vai se aproximando cada vez mais de zero!
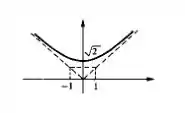
Como , isso significa que à medida que cresce, o gráfico de vai encostando por cima do gráfico de .
Esse é o mesmo raciocício feiro na questão . Se você não lembra, dá uma espiadinha lá =D
Passo 2
O domínio dessa função vão ser todos os reais, pois não há valor de capaz de tornar inválida a função. O domínio pode ser expresso da seguinte forma:
Passo 3
E o esboço? Bom, ele vai ser bem parecido com o esboço do gráfico do exercício , no entanto o ponto no qual a função vai cortar o eixo será outro:
Então temos . Assim o esboço vai ser:
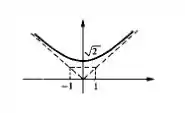
Certo? Vamos pra próxima?
Resposta
