Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 16
- Verifique que . Conclua que à medida que cresce a diferença se aproxima de zero.
- Esboce o gráfico de
Passo 1
a) Humm vamos ver, primeiro temos que provar que né?
Vamos fazer isso mexendo no lado esquerdo da função e começar multiplicando pelo seu conjugado em cima e embaixo ok?
Lembrando que o conjugado de é .
Multiplicando,
Aplicando o nosso querido “chuveirinho”, a propriedade distributiva hehe:
Ajeitando, ficamos com,
No numerador temos , então, simplificando, temos
Uhuuu, então provamos que :P
Passo 2
Agora vamos provar que à medida que cresce, a diferença se aproxima de zero.
Acabamos de provar que
Quando vai crescendo, o denominador de vai ficando cada vez maior né?
Agora mano, pensa comigo, vamos pensar nas seguintes divisões:
Reparou que conforme a gente vai aumentando o denominador, o resultado da divisão vai diminuindo?
É isso que vamos analisar aqui, temos
Quando vamos aumentando o denominador (já que está crescendo), estamos diminuindo o resultado da divisão, que é .
Portanto, realmente, conforme cresce, o diminui ;)
Passo 3
b) Agora vamos esboçar o gráfico da função . Vamos ver primeiro onde a função cruza o eixo e depois ver onde cruza o eixo .
A função cruza o eixo nos pontos onde . Calculando,
Opa, não tem solução pra né? Não tem como um número ao quadrado resultar em um valor negativo hehe Então, essa função não corta o eixo .
Agora vamos ver se ela corta o eixo substituindo :
Então sabemos que pertence ao gráfico.
Passo 4
Agora a estratégia será substituir valores arbitrários poistivos e negativos.
Vamos encontrar alguns pontos pertencentes a esse gráfico para aí podermos plotar:
Se
Se
Se
Se
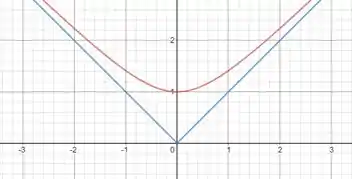
Usando um programa de geração gráfica temos a curva em vermelho:
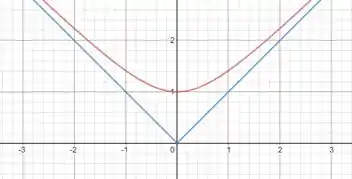
Galera, ainda vamos ver isso melhor, mas já vamos observando que o gráfico acima nunca encosta na função (representada em azul)
Resposta
a) Demonstração
b)
