Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.Revisão - Ex. 15c
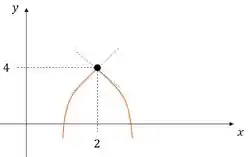
Em cada parte, esboce uma curva contínua com as propriedades indicadas:
(c) com , ,
Passo 1
A ideia aqui é passar por cada característica que o enunciado dá para esboçar o gráfico de uma função e representar essa característica no gráfico.
A gente não precisa dizer quem ela é, só fazer o desenho.
Vamos lá!
Passo 2
A primeira coisa que ele diz é que a função passa pelo ponto . Fica assim:
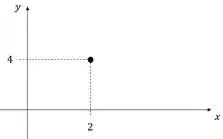
Outra coisa que ele diz sobre esse ponto é que o limite da derivada vai para antes do ponto e depois do ponto.
Isso quer dizer que a derivada não é contínua nesse ponto. E temos um “bico” quando a função passa por esse ponto.
Temos que lembrar disso na hora de desenhar o gráfico. Vamos desenhar duas retas tangentes auxiliares. Uma como e uma com :
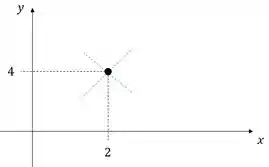
Passo 3
Ele diz se o valor da derivada segunda antes e depois desse ponto é positiva ou negativa. Isso diz para a gente a concavidade da curva.
Como para valores de diferentes de
A concavidade da função nesses valores vai estar voltada para baixo.
Traçando uma curva com essas características no nosso gráfico:
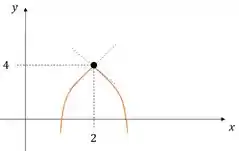
Prontinho!
Resposta
