7- Em cada parte, esboce o gráfico de uma função que satisfaça as condições propostas.

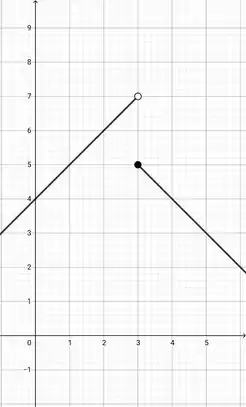
a) é contínua em toda parte, exceto em , onde é contínua à direita.

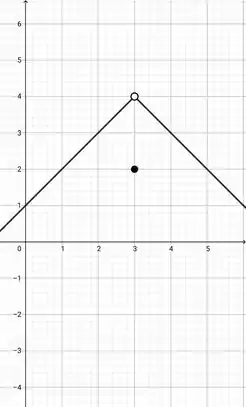
b) tem um limite bilateral em , mas não é contínua naquele ponto.

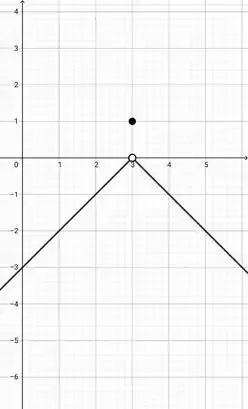
c) não é contínua em , mas se seu valor em , for mudado de para , torna-se contínua em .

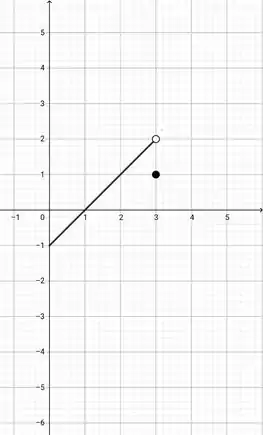
d) é contínua no intervalo e está definida no intervalo fechado ; mas não é contínua no intervalo .

b)Caraaa, limite bilateral significa que , certo ? Mas como a função não é contínua em , o nosso limite vai ser existir, mas ele não será igual a , ou seja, temos que definir outro valor para .

Nós podemos definir a seguinte função:

Esse é o nosso gráfico:

b)Bom, aqui nós temos uma descontinuidade em , o valor que nós esperávamos para seria zero, mas a nossa função vai ter outro valor definido para esse ponto. Dessa forma,

Assim, temos o seguinte gráfico:

d)Ebaaa, chegamos na última !!!

Aqui, nós temos uma função definida no intervalo , mas que tem uma descontinuidade em . Ou seja, temos que definir um valor diferente daquele que nós obteríamos utilizando a expressão da nossa função. Ok?

Dessa forma, podemos escrever isso:

Portanto,temos o seguinte gráfico: