Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.1 - Ex. 7
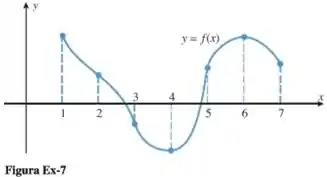
Em cada parte, use o gráfico de na figura abaixo para encontrar a informação requisitada.
(a) Encontre os intervalos nos quais é crescente.
(b) Encontre os intervalos nos quais é decrescente.
(c) Encontre os intervalos abertos nos quais é côncava para cima.
(d) Encontre os intervalos abertos nos quais é côncava para baixo.
(e) Encontre todos os valores de nos quais tem um ponto de inflexão.
Passo 1
(a) vai ser crescente quando, da esquerda pra direita, a função estiver “subindo”, ou seja, crescendo. É fácil verificar isso pelo gráfico. Os intervalos serão:
e .
Passo 2
(b)De forma análoga, vai ser decrescente quando, da esquerda pra direita, a função estiver “descendo”, logo, decrescendo. Os intervalos em que isso ocorre são:
, , e .
Passo 3
(c)A função vai ter concavidade, seja pra cima ou pra baixo, nos trechos em que ela não se comportar como uma linha reta (função afim). Selecionamos os intervalos em que a função tem concavidade voltada pra cima em:
, e (
Passo 4
(d)Da mesma forma que em (c), avaliamos os intervalos com concavidade pra baixo em:
, ,
Passo 5
(e)Aqui temos um pequeno trabalho de visualização. Os pontos de inflexão são os pontos em que ocorre a mudança da concavidade do gráfico. No caso desse gráfico, esses pontos ocorrem em:
, e
Resposta
(a) e .
(b), , e .
(c), e
(d), ,
(e), e