Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.6 - Ex. 11
Em cada um dos Problemas 11 e 12:
(a) Encontre os autovalores do sistema dado.
(b) Escolha um ponto inicial (diferente da origem) e desenhe a trajetória correspondente no plano .
(c) Para a sua trajetória encontrada em (b), desenhe os gráficos de e em função de .
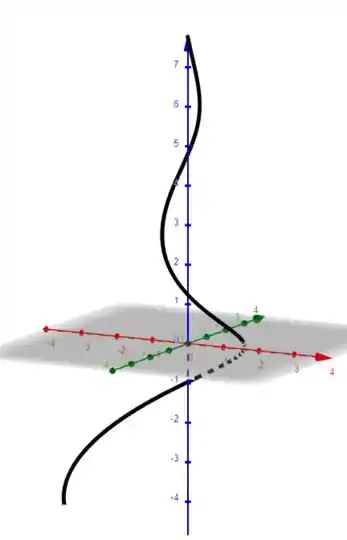
(d) Para a sua trajetória encontrada em (b), desenhe o gráfico correspondente no espaço tridimensional .
Passo 1
Procurando os autovalores dessa matriz nós teremos:
Fazendo então essa determinante teremos:
O que nos dá uma equação igual a:
Cujas raízes serão:
Passo 2
E o autovetor desse sistema para será:
E pela segunda linha vemos que há uma relação entre ambas igual a:
Então uma solução para essa equação seria e , portanto o autovetor seria:
Nos dando então uma solução igual a:
Como , e o cosseno é uma função par e o seno uma função ímpar então:
Logo:
Separando parte real da parte imaginária nós teremos:
Então a solução geral fica como:
Você pode encontrar diversas soluções parciais.
Passo 3
Considerando que o termo inicial em será:
Então:
Então:
Dando uma solução geral igual a:
Ou:
E por isso vamos considerar e . Isso nos dá uma trajetória em nós teremos:
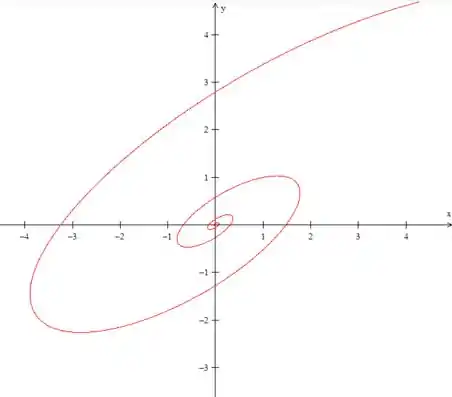
Passo 4
Plotando o gráfico de e nós teremos:
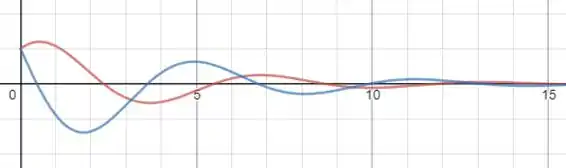
Onde é a curva vermelha e a azul.
Passo 5
Agora para nós teremos:
