Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.6 - Ex. 25

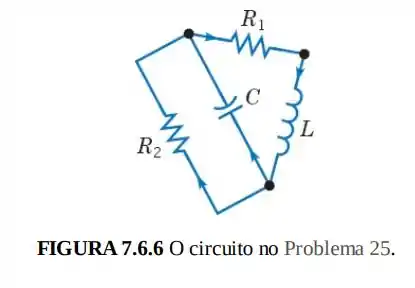
25- Considere o circuito elétrico na Figura 7.6 . 6 . Suponha que R 1 = R 2 = 4   Ω ,   C = 1 2 F e L = 8 H

( a ) Mostre que esse circuito é descrito pelo sistema de equações diferenciais

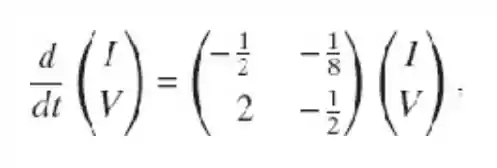
Em que I é a corrente passando no indutor e V é a queda de tensão através do capacitor. Sugestão: Veja o Problema 20 da Seção 7.1

( b ) Encontre a solução geral das Eqs ( i ) em termos de funções reais

( c ) Encontre I ( t ) e V ( t ) se I 0 = 2   A e V 0 = 3   V

( d ) Determine os valores limites de I ( t ) e V ( t ) quando t → ∞ . Esses valores dependem das condições iniciais?

Passo 1

Pelo problema 20 da seção 7.1 nós descobrimos que:

d d t I V = - R 1 / L - 1 / L 1 / C - 1 / C R 2 I V

Portanto como R 1 = R 2 = 4   Ω ,   C = 1 2 F e L = 8 H (sim a questão acabou comendo a informação de que o capacitor vale 1 2 F , se não há esse valor, então não terá como mostrar a letra a ) ,deixando a nossa matriz da seguinte forma:

d d t I V = - 1 / 2 - 1 / L 1 1 2 - 1 4 × 1 2 I V

d d t I V = - 1 / 2 - 1 8 2 - 1 2 I V

Passo 2

Encontrando os autovalores dessa matriz nós teremos:

det ⁡ - 1 2 - r - 1 8 2 - 1 2 - r = 0

Então:

- 1 2 - r 2 + 1 4 = 0

r 2 + r + 1 4 + 1 4 = 0

r 2 + r + 1 2 = 0

Isso nos dá raízes iguais a:

r 1 ; r 2 = - 1 ± 1 - 4 × 1 2 2 = - 1 2 ± 1 2 i

Passo 3

Para r = - 1 2 - 1 2 i nós teremos o seguinte autovetor:

- 1 2 + 1 2 + 1 2 i - 1 8 2 - 1 2 + 1 2 + 1 2 i ξ 1 ξ 2 = 0

Logo:

1 2 i - 1 8 2 1 2 i ξ 1 ξ 2 = 0

Pela primeira linha nós vemos que:

1 2 i ξ 1 - 1 8 ξ 2 = 0

Isso nos dá:

4 i ξ 1 = ξ 2

Uma solução será ξ 1 = 1 e ξ 2 = 4 i , nos dando um autovetor igual a:

ξ = 1 4 i

Então a solução por parte desse autovalor será:

x 1 = 1 4 i e - 1 2 + 1 2 i t = 1 4 i e - t 2   e - i t 2

O valor de   e - i t 2 será cos ⁡ t 2 - i   s e n t 2 então a solução será:

x 1 = 1 4 i e - t 2 cos ⁡ t 2 - i   s e n t 2

Então separando a parte real da imaginária nós teremos:

x 1 = cos ⁡ t 2 4 s e n t 2 e - t 2 + i - s e n t 2 4 cos ⁡ t 2 e - t 2

Então a solução geral será igual a:

x = c 1 cos ⁡ t 2 4 s e n t 2 e - t 2 + c 2 - s e n t 2 4 cos ⁡ t 2 e - t 2

Passo 4

Como x = I V e se aplicarmos a condição inicial em t = 0 e igual a x = 2 3 , então:

2 = c 1

3 = 4 c 2 → c 2 = 3 4

Então a equação de I ( t ) e de V ( t ) serão iguais a:

I t = e - t 2 2 cos ⁡ t 2 - 3 4 s e n t 2

V t = e - t 2 8 s e n t 2 + 3 cos ⁡ t 2

Como as duas equações tem o termo e - t 2 então para t → ∞ logo as duas equações tenderão a zero (ou a origem pois x = 0,0 T )

Resposta

b )   x = c 1 cos ⁡ t 2 4 s e n t 2 e - t 2 + c 2 - s e n t 2 4 cos ⁡ t 2 e - t 2

c )   I t = e - t 2 2 cos ⁡ t 2 - 3 4 s e n t 2

V t = e - t 2 8 s e n t 2 + 3 cos ⁡ t 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos Problemas 7 e 8 : ( a ) Encontre a solução geral do sistema de equações dado ( b ) Desenhe um campo de direções e algumas das trajetórias. Em cada um desses, a matriz de coeficientes te
Em cada um dos problemas de 1 a 6 : ( a ) Encontre a solução geral do sistema de equações dado e descreva o comportamento das soluções quando t → ∞ ( b ) Desenhe um campo de direções e faça o gráfico
Referindo-se ao Problema 19 , resolva o sistema de equações dado em cada um dos problemas de 20 a 23 . Suponha que t0 t x ' = 2 - 1 3 - 2 x
Em cada um dos problemas de 9 a 14 , encontre a solução geral do sistema de equações dado. x ' = 1 1 1 2 1 - 1 - 8 - 5 - 3 x
Em cada um dos problemas de 1 a 6 : ( a ) Encontre a solução geral do sistema de equações dado e descreva o comportamento das soluções quando t → ∞ ( b ) Desenhe um campo de direções e faça o gráfico