Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.5 - Ex. 26
Em cada um dos problemas de a , são dados os autovalores e autovetores de uma matriz . Considere o sistema correspondente .
Esboce um retrato de fase do sistema
Esboce a trajetória que contém o ponto inicial
Para a trajetória no item . Esboce os gráficos de e de em função de no mesmo conjunto de eixos.
Passo 1
Vamos encontrar a matriz desse sistema para que possamos plotar os gráficos que a questão pede:
Supondo que a matriz é
Nós teremos as seguintes relações com os autovalores e os autovetores:
A primeira matriz nos dá equações iguais a:
Já a segunda:
Comparando a primeira equação com a terceira e a segunda com a quarta nós teremos:
Portanto a matriz será igual a:
Nos dando um retrato de fase igual a:
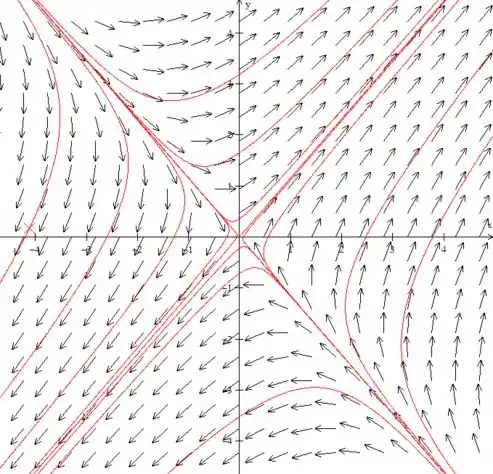
Passo 2
Fazendo e nós teremos :
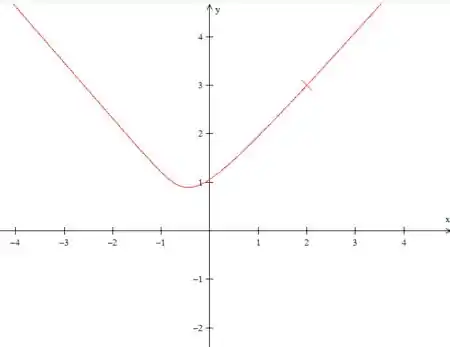
Onde é a horizontal e a vertical. Porém como a reta é crescente onde está o ponto então só teremos a parta a direita desse ponto. Ou seja:
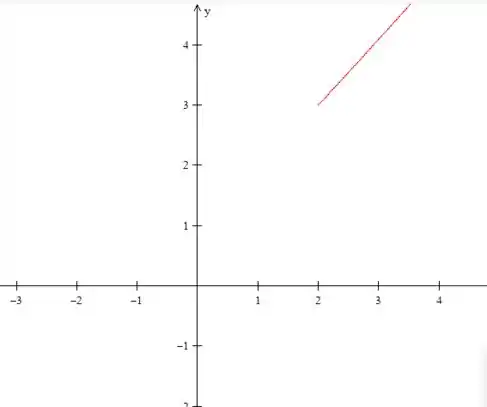
Passo 3
Os valores de e em relação ao tempo podem ser encontradas da seguinte forma:
Portanto:
Como o ponto inicial é em e e então:
Resolvendo esse sistema teremos:
Nos deixando com:
Plotando esses dois gráficos nós teremos:
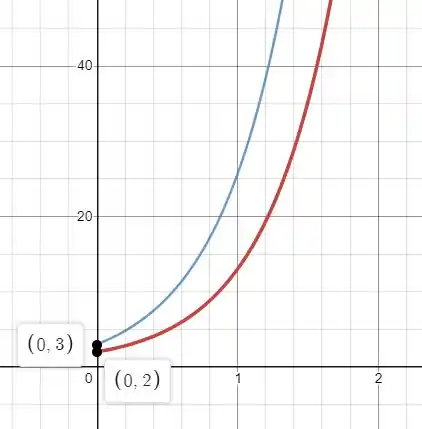
Onde a curva vermelha é e azul . E essa curva caracteriza um sistema instável. Assim como a figura do retrato de fase.