Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.2 - Ex. 13
Em cada um dos problemas de 13 a 18:
(a) Esboce o gráfico da função dada por três períodos.
(b) Encontre a série de Fourier da função dada.
Passo 1
(a) O gráfico pode ser dado por um CAS (caso do Geogebra, Desmos, Symbolab).
O gráfico esboçado é dado por:
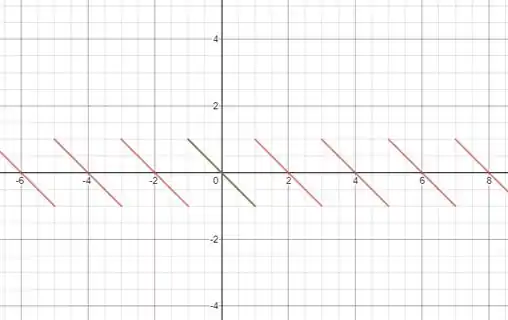
Passo 2
(b) Esta função é periódica com o período .
Assim, neste caso, da fórmula (1) na página 597 e do problema são os mesmos, e a série de Fourier tem a forma:
Observe que é uma função ímpar Conforme descrito em (8) na página 616, temos:
Então:
Logo:
Finalmente, substituímos os coeficientes pela fórmula e obtemos:
Resposta
Exercícios de Livros Relacionados
Em cada um dos problemas de 19 a 24: (a) Esboce o gráfico da função dada por três períodos. (b) Encontre a série de Fourier da função dada. f x = - 1,- 2 ≤ x0 1 ,0 ≤ x2 f x + 4 = f ( x )
Considere a função f definida no problema 24, e seja e m = f x - s m ( x ) . f x = 0 , - 3 ≤ x ≤ 0 , x 2 3 - x , 0x3 (a) Faça o gráfico de e m ( x ) em função de x para 0 ≤ x ≤ 3 para diversos valores
Considere a função f definida no problema 21, e seja e m = f x - s m ( x ) . f x = x 2 2 ,- 2 ≤ x2 f x + 4 = f ( x ) (a) Faça o gráfico de e m ( x ) em função de x para 0 ≤ x ≤ 2 para diversos valores
Se f for diferenciável e periódica com período T , mostre que f ' também é periódica com período T . Determine se F x = ∫ 0 x f t d t É sempre periódica.
f x = x ,- 1 ≤ x1 f x + 2 = f ( x ) (a) Esboce o gráfico da função dada por três períodos.(b) Encontre a série de Fourier para a equação dada.(c) Faça o gráfico da soma parcial s m ( x ) em função de