Considere a função definida no problema 21, e seja .
(a) Faça o gráfico de em função de para para diversos valores de .
(b) Encontre o menor valor de para o qual para todo .
Passo 1
Antes de começar, vamos retomar a série de Fourier obtida para o problema 21:
Em poucas palavras, o exercício nos pede para verificar o quanto a série de Fourier se aproxima da função original e, para isso, iremos calcular a diferença entre os valores de e . Conforme vamos aumentando o número de termos () da série o esperado é que essa diferença diminua. Por essa razão, o item (b) nos pede para continuar incrementando o valor de até que seja atingida uma diferença de . Tudo bem até aqui? Vamos lá então.
Passo 2
Para resolver os dois itens precisamos do auxílio de uma ferramenta gráfica, como o Excel. O primeiro passo é fazer uma tabela de para vários valores no intervalo . Para este exemplo, usar valores espaçados de 0,1 é o suficiente, ou seja, plotar valores para 0, 0.1, 0.2,..., 1.8, 1.9 e 2. Em seguida, devemos calcular os coeficientes da série de Fourier e para variando de até um valor de arbitrário. Para o nosso caso, é um valor razoável.
Depois de calcular os coeficientes, iremos aplicar a função para os mesmos pontos em que aplicamos . O passo seguinte, é fazer a diferença para todos os pontos. A função é dada pela soma de todas as diferenças no intervalo .
Passo 3
O gráfico de em função de é apresentado a seguir:
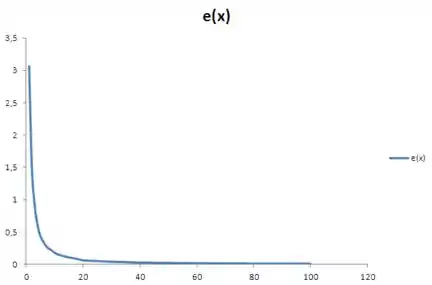
Assim como o esperado, ao aumentar o número de termos da série a diferença , ou seja, para , a série de Fourier representa perfeitamente a função .
O item (b) nos pede para encontrar em que . Pela tabela de valores de :

Podemos ver que para em torno de 90, o valor de é atingido.
Resposta
Ei, a resposta está no passo a passo :)