Em cada um dos problemas de 9 a 20:
(a) Encontre a solução do problema de valor inicial dado em forma explícita.
(b) Desenhe o gráfico da solução.
(c) Determine (pelo menos aproximadamente) o intervalo no qual a solução está definida.
,
Passo 1
Olá, tudo bem? Vem comigo que vou te ajudar a resolver essa atividade.
O problema de valor inicial (PVI) dado é uma equação diferencial ordinária (EDO) de variáveis separáveis:
Passo 2
- A EDO acima, é do tipo que pode separar para calculcar a solução. Agora, vamos deixar tudo que tem y de um lado e tudo que tem do outro lado. Antes, vamos substituir o y’ por .
Assim, temos:
Agora para termos uma equação dependendo de y e de x, basta integrar dos dois lados
Integrando dos dois lados, temos:
No enunciado há uma informação de que . Vamos escrever a seguir a solução final que encontramos da EDO.
Ao substituir a informação encontramos o valor da constante C. Logo, temos:
Assim, a equação é:
Passo 3
b)
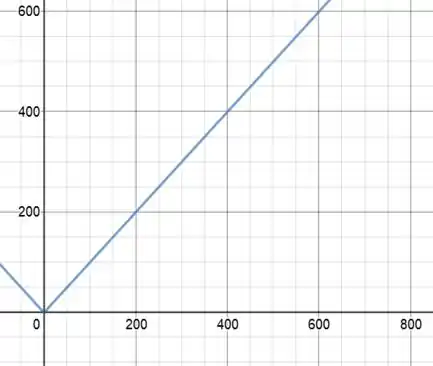
Passo 4
- Temos como equação final da EDO o seguinte:
O argumento da raiz quadrada na solução explícita deve ser não-negativo:
Isso implica em:
O denominador da EDO original não pode ser zero:
Substitua na solução implícita para encontrar os valores de que causam essa singularidade:
Os pontos de singularidade ocorrem em . No entanto, estes são exatamente os pontos onde a função sob a raiz quadrada é zero, o que define o limite do domínio.
Como é positivo e a solução cresce para , ela nunca atingirá . A solução é limitada pelo ponto onde a raiz quadrada se anula.
O intervalo de definição da solução que contém é: