O método esboçado no Problema 30 pode ser usado em qualquer equação homogênea. Ou seja,
a substituição y = xυ(x) transforma uma equação homogênea em uma equação separável. Esta
última equação pode ser resolvida por integração direta, e depois a substituição de υ por y/x
fornece a solução da equação original. Em cada um dos problemas de 31 a 38:
(a) Mostre que a equação dada é homogênea.
(b) Resolva a equação diferencial.
(c) Desenhe um campo de direções e algumas curvas integrais. Elas são simétricas em relação
à origem?
Passo 1
Fala aí! tudo certinho?
Nesse problema foi dada a equação:
E nosso objetivo é mostrar que essa equação é homogênea, encontrar sua solução e desenhar o campo de direções e simetria.
Tem ideia de como fazemos isso?
Para verificar se a equação é homogênea, temos que verificar se
Em que .
Depois calculamos a solução desse sistema substituindo .
Bora começar!
Passo 2
Primeiro vamos verificar se a equação é homogênea.
Se dividirmos o numerador e o denominador por , vamos obter
Então se ...
Logo, a equação é homogênea!
Passo 3
Agora temos que calcular a solução dessa equação...
Se , pela regra do produto temos:
Igualando a , temos:
Separando as variáveis:
Reescrevendo o lado esquerdo em frações parciais, chegamos em:
Ou seja:
Integrando nos dois lados:
Show?
Passo 4
Podemos reorganizar essa equação como:
Elevando os dois lados a e aplicando a propriedade das exponenciais:
Voltando ...
Simplificando os expoentes...
E multiplicando ambos os lados por ...
Tranquilo até aqui?
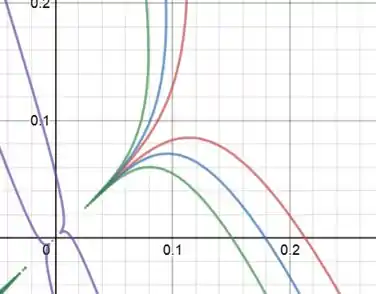
Passo 5
C) As retas abaixo foram construídas quando C obteve tais valores:
vermelha – C =2
azul – C = 4
verde – C = 8
roxa - C = 100000
Ou seja, a medida que o valor de C aumenta mais a curva se aproxima da origem. As curvas são simétricas em relação a origem.
Resposta
É Homogenea.