Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 5.2 - Ex. 28

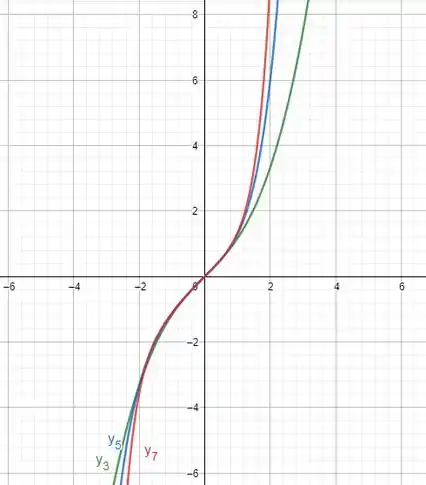
Em cada um dos problemas de 23 a 28, faça o gráfico de diversas somas parciais da solução em série do problema de valor inicial dado em torno de x = 0, obtendo, assim, gráficos análogos aos ilustrados nas Figuras de 5.2.1 a 5.2.4.

1 - x y ' ' + x y ' - 2 y = 0 ,   y 0 = 0 ,   y ' 0 = 1

Passo 1

Beleza! Para encontrar os primeiros termos da solução em torno de x = 0, nós vamos procurar por uma solução em torno de zero no formato de uma série de potência, então, teremos:

y = ∑ n = 0 + ∞ a n x n

Então, derivando essa expressão para obter y ' e y ' ' , temos:

y ' = ∑ n = 0 + ∞ n + 1 a n + 1 x n = ∑ n = 1 + ∞ n a n x n - 1

y ' ' = ∑ n = 0 + ∞ n + 2 n + 1 a n + 2 x n = ∑ n = 2 + ∞ n n - 1 a n x n - 2

Agora vamos substituir esses termos na equação fornecida no enunciado, obtendo:

1 - x y ' ' + x y ' - 2 y = 0

1 - x ∑ n = 2 + ∞ n n - 1 a n x n - 2 + x ∑ n = 1 + ∞ n a n x n - 1 - 2 ∑ n = 0 + ∞ a n x n = 0

E, rearranjando os termos, chegamos em:

∑ n = 2 + ∞ n n - 1 a n x n - 2 - ∑ n = 2 + ∞ n n - 1 a n x n - 1 + ∑ n = 2 + ∞ n a n x n - 2 ∑ n = 0 + ∞ a n x n = 0

∑ n = 0 + ∞ n + 2 n + 1 a n + 2 x n - ∑ n = 1 + ∞ n n + 1 a n + 1 x n + ∑ n = 1 + ∞ n a n x n - 2 ∑ n = 0 + ∞ a n x n = 0

Agora, reescrevendo para que todos os somatórios começem de n = 1 , temos:

2 a 2 + ∑ n = 1 + ∞ n + 2 n + 1 a n + 2 x n - ∑ n = 1 + ∞ n n + 1 a n + 1 x n + ∑ n = 1 + ∞ n a n x n - 2 a 0 - 2 ∑ n = 1 + ∞ a n x n = 0

E, agora, agrupando os somatórios, temos:

2 a 2 - 2 a 0 + ∑ n = 1 + ∞ n + 2 n + 1 a n + 2 - n n + 1 a n + 1 + n - 2 a n x n = 0

Passo 2

Agora, como a equação obtida é igual a zero, temos que os termos dentro e fora do somatório devem ser iguais a zero, dessa forma, obtemos um sistema com duas equações, sendo elas:

2 a 2 - 2 a 0 = 0 n + 2 n + 1 a n + 2 - n n + 1 a n + 1 + n - 2 a n = 0

Então, da segunda equação, temos:

n + 2 n + 1 a n + 2 - n n + 1 a n + 1 + n - 2 a n = 0

n + 2 n + 1 a n + 2 = n n + 1 a n + 1 - n - 2 a n → a n + 2 = n n + 1 a n + 1 - n - 2 a n n + 2 n + 1

Essa é a fórmula de recorrência. Agora analisando a primeira equação do nosso sistema, então, os primeiros termos serão:

a 0 + 2 = 0 0 + 1 a 0 + 1 - 0 - 2 a 0 0 + 2 0 + 1 → a 2 = a 0

a 1 + 2 = 1 1 + 1 a 1 + 1 - 1 - 2 a 1 1 + 2 1 + 1 → a 3 = 2 a 2 + a 1 6 → a 3 = 2 a 0 + a 1 6

a 2 + 2 = 2 2 + 1 a 2 + 1 - 2 - 2 a 2 2 + 2 2 + 1 → a 4 = 6 a 3 12 = 1 2 2 a 0 + a 1 6 → a 4 = 2 a 0 + a 1 12

a 3 + 2 = 3 3 + 1 a 3 + 1 - 3 - 2 a 3 3 + 2 3 + 1 → a 5 = 12 a 4 - a 3 20 = 12 2 a 0 + a 1 12 - 2 a 0 + a 1 6 20

a 5 = 2 a 0 + a 1 24

a 4 + 2 = 4 4 + 1 a 4 + 1 - 4 - 2 a 4 4 + 2 4 + 1 → a 6 = 20 a 5 - 2 a 4 30 = 20 2 a 0 + a 1 24 - 2 2 a 0 + a 1 12 30

a 6 = 2 a 0 + a 1 45

a 5 + 2 = 5 5 + 1 a 5 + 1 - 5 - 2 a 5 5 + 2 5 + 1 → a 7 = 30 a 6 - 3 a 5 42 = 30 2 a 0 + a 1 45 - 3 2 a 0 + a 1 24 42

a 7 = 26 a 0 + 13 a 1 1008 → a 7 = 13 2 a 0 + a 1 1008

Então a solução será:

y x = a 0 + a 1 x + a 0 x 2 + 2 a 0 + a 1 6 x 3 + 2 a 0 + a 1 12 x 4 + 2 a 0 + a 1 24 x 5 + 2 a 0 + a 1 45 x 6 + 13 2 a 0 + a 1 1008 x 7 + …

Então, colocando os termos a 0 e a 1 em evidência, temos:

y x = a 0 1 + x 2 + x 3 3 + x 4 6 + x 5 12 + 2 x 6 45 + 26 x 7 1008 + … + a 1 x + x 3 6 + x 4 12 + x 5 24 + x 6 45 + 13 x 7 1008 + …

Passo 3

Então, a derivada da solução será:

y ' x = a 0 2 x + x 2 + 2 x 3 3 + 5 x 4 12 + 12 x 5 45 + 182 x 6 1008 + … + a 1 1 + x 2 2 + x 3 3 + 5 x 4 24 + 6 x 5 45 + 91 x 6 1008 + …

Então, substituindo as condições de contorno iniciais fornecidas no enunciado, temos:

y 0 = 0 → a 0 1 + 0 2 + 0 3 3 + 0 4 6 + 0 5 12 + 2 ( 0 ) 6 45 + 26 ( 0 ) 7 1008 + … + a 1 0 + 0 3 6 + 0 4 12 + 0 5 24 + 0 6 45 + 13 ( 0 ) 7 1008 + … = 0

a 0 = 0

y ' 0 = 1 → a 0 2 ( 0 ) + 0 2 + 2 ( 0 ) 3 3 + 5 ( 0 ) 4 12 + 12 ( 0 ) 5 45 + 182 ( 0 ) 6 1008 + … + a 1 1 + 0 2 2 + 0 3 3 + 5 ( 0 ) 4 24 + 6 ( 0 ) 5 45 + 91 ( 0 ) 6 1008 + … = 1

a 1 = 1

Então, substituindo os valores de a 0 e a 1 , a solução será dada por:

y x = 0 1 + x 2 + x 3 3 + x 4 6 + x 5 12 + 2 x 6 45 + 26 x 7 1008 + … + 1 x + x 3 6 + x 4 12 + x 5 24 + x 6 45 + 13 x 7 1008 + …

y x = x + x 3 6 + x 4 12 + x 5 24 + x 6 45 + 13 x 7 1008 + …

Passo 4

Então, o gráfico com as soluções parciais será:

Resposta

y x = x + x 3 6 + x 4 12 + x 5 24 + x 6 45 + 13 x 7 1008 + …

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use série de potência para resolver a equação diferencial. y ' - y = 0
Use série de potência para resolver a equação diferencial. y ' = x 2 y
Use série de potência para resolver a equação diferencial. y ' = x y
Use série de potência para resolver a equação diferencial. y ' ' = x y
Nos problemas 1-14, para cada equação diferencial, encontre duas soluções em série de potências linearmente independentes em torno do ponto ordinário x = 0 .3. y ' ' - 2 x y ' + y = 0