Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.5 - Ex. 27
Em cada um dos problemas de a , são dados os autovalores e autovetores de uma matriz . Considere o sistema correspondente .
Esboce um retrato de fase do sistema
Esboce a trajetória que contém o ponto inicial
Para a trajetória no item . Esboce os gráficos de e de em função de no mesmo conjunto de eixos.
Passo 1
Começando pela matriz que tem a seguinte forma:
E pelos autovalores e autovetores nós podemos encontrar ela como:
Fazendo a multiplicação vetorial temos que:
Isso nos dará valores iguais a:
Isso nos dará uma matriz igual a:
Então o retrato de fase será igual a:
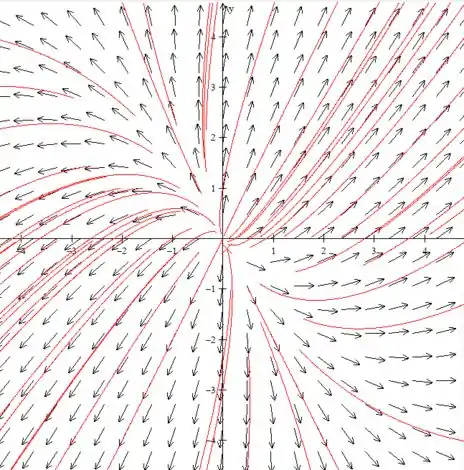
Isso é um sistema bem instável hahaha
Passo 2
O ponto estará representado da seguinte forma:
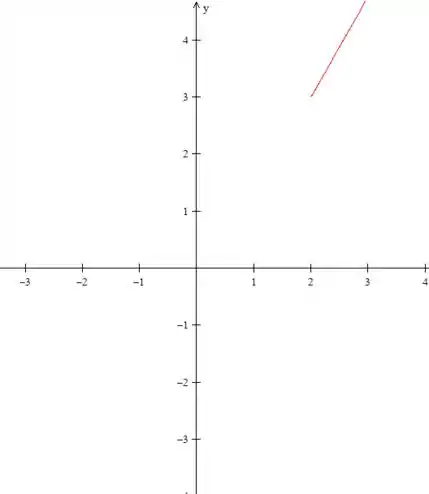
Passo 3
Nossa representação de e em relação ao tempo será:
Aplicando o ponto em em e nós teremos:
Então como em todas as outras questões anteriores dessa série:
Nos dando equações iguais a:
Plotando os dois resultados teremos:
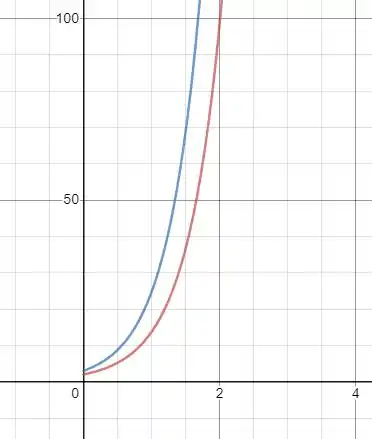
Nos mostrando que o sistema é instável.
Note que para que tenhamos um sistema instável basta um dos auto valores ser positivo, e note em cada exercício (da a ) a influência dos autovalores nos gráficos de e e na matriz também.