Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.5 - Ex. 2
Em cada um dos problemas de a :
Encontre a solução geral do sistema de equações dado e descreva o comportamento das soluções quando
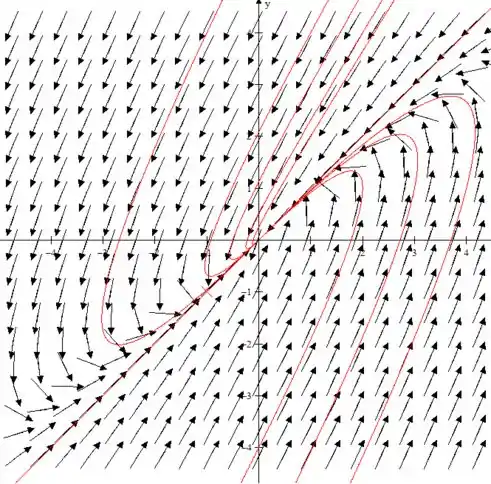
Desenhe um campo de direções e faça o gráfico de algumas trajetórias do sistema
Passo 1
A solução geral dessas equações diferenciais tem a cara igual a:
Onde e
E nós encontramos (que são os auto valores) e (que são os auto vetores), e esses parâmetros podem ser descobertos ao fazer:
Onde a parte nula é a parte do auto valor e que será:
Fazendo o determinante dessa matriz temos:
Então os auto valores serão:
Passo 2
Substituindo os auto valores na matriz teremos os autovetores e que serão para :
Fazendo a multiplicação vetorial nós teremos:
E e se correlacionam de forma que:
Então o autovetor associado a será:
Logo a primeira solução será:
Passo 3
E o auto vetor para será:
Então pela multiplicação vetorial temos
Então o segundo autovetor (associado a ) será:
Nos dando uma segunda solução igual a:
Logo a solução geral da EDO será a soma das duas soluções e será:
Passo 4
Desenhando o campo de direções dessa EDO nós iremos ter:
