Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.6 - Ex. 26
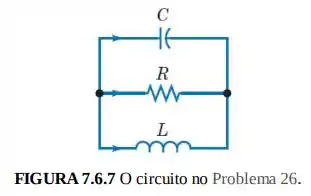
O circuito elétrico ilustrado na Figura é descrito pelo sistema de equações diferenciais
em que é a corrente passando no indutor e V é a queda de tensão através do capacitor. Essas equações diferenciais foram deduzidas no Problema 19 da Seção 7.1.
Mostre que os autovalores da matriz de coeficientes são reais e distintos se ; mostre que são complexos conjugados se .
Suponha que e .Encontre a solução geral do sistema nesse caso.
Encontre e se e .
Para o circuito no item , determine os valores limites de e quando . Esses valores limites dependem das condições iniciais?
Passo 1
Os autovalores dessa matriz serão encontrados fazendo a determinante igual a:
Então:
Portanto:
E as raízes serão:
E se as raízes são reais e distintas então:
E se as raízes são complexas então:
Então:
Passo 2
Para os valores dados na letra nós teremos:
e , então teremos raízes complexas, portanto os autovalores serão:
E a matriz de coeficientes fica:
Encontrando o autovetor para nós teremos:
Pela primeira linha nós temos a relação:
A solução para essa equação pode ser e , logo a solução causada por esse autovalor será:
E que será escrita por:
Separando a parte real da imaginária nós teremos:
E a solução geral portanto será:
Passo 3
Aplicando a condição inicial em nós teremos:
Portanto e isso vai nos dar uma equação geral igual a:
Essa solução deve ser encontrada para todos os autovetores diferentes.
E como tanto quanto tem o termo , então quando tenderão a zero.