Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 8.5 - Ex. 2
Em cada um dos problemas de 1 a 6, determine valores aproximados da solução do problema de valor inicial dado em . Compare os resultados obtidos por métodos diferentes e tamanhos de passos diferentes.
(a) Use o método de Euler com
(b) Use o método de Runge-Kutta com
(c) Use o método de Runge-Kutta com
Passo 1
As fórmulas que usaremos no exercício serão e
O método de Runge-Kutta pode ser generalizado pra sistemas:
As demais pertencem a (7):
Faremos as aproximações em , fazendo alterações a cada índice.
Passo 2
Para este problema, temos e . Agora use as fórmulas (4) e (5) e as condições iniciais para obter e
Além disso, nós temos.
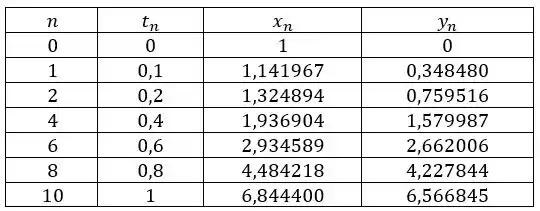
Temos e . Vamos montar uma tabelinha marota, indicando o que nós chamaremos de iteração, a cada passo de até , e os resultados se atualizam a cada iteração, repetindo o processo que calculamos aqui encima:
Passo 3
Para este problema, temos e . Agora use as fórmulas (6) e (7) e as condições iniciais para obter
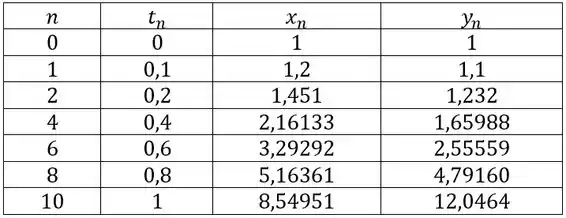
Temos e . Vamos montar uma tabelinha marota, indicando o que nós chamaremos de iteração, a cada passo de até , e os resultados se atualizam a cada iteração, repetindo o processo que calculamos aqui encima:
Passo 4
Para este problema, temos e . Agora use as fórmulas (6) e (7) e as condições iniciais para obter
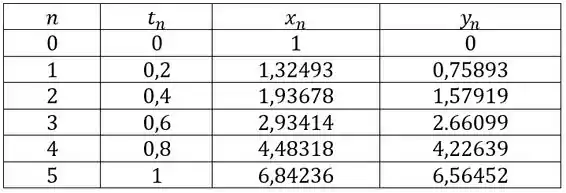
Temos e . Vamos montar uma tabelinha marota, indicando o que nós chamaremos de iteração, a cada passo de até , e os resultados se atualizam a cada iteração, repetindo o processo que calculamos aqui encima:
