Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 8.5 - Ex. 7
Considere o problema do exemplo com as condições iniciais Use o método de Runge-Kutta para encontrar valores aproximados da solução desse problema no intervalo . Comece com e depois repita os cálculos com ; . . . , cada um como a metade do anterior. Continue o processo até os cinco primeiros dígitos da solução em permanecerem constantes para tamanhos sucessivos de passos. Determine se esses dígitos são precisos comparando-os com a solução exata dada nas Eqs. (10) no texto.
Passo 1
As fórmulas que usaremos no exercício serão e
O método de Runge-Kutta pode ser generalizado pra sistemas:
As demais pertencem a (7):
Passo 2
Para este problema, temos e . Agora use as fórmulas (6) e (7) e as condições iniciais para obter
Temos e . Vamos montar uma tabelinha marota, indicando o que nós chamaremos de iteração, a cada passo de até , e os resultados se atualizam a cada iteração, repetindo o processo que calculamos aqui encima:
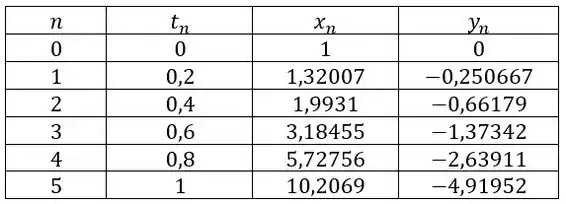
Passo 3
Para este problema, temos e . Agora use as fórmulas (6) e (7) e as condições iniciais para obter
Temos e . Vamos montar uma tabelinha marota, indicando o que nós chamaremos de iteração, a cada passo de até , e os resultados se atualizam a cada iteração, repetindo o processo que calculamos aqui encima:
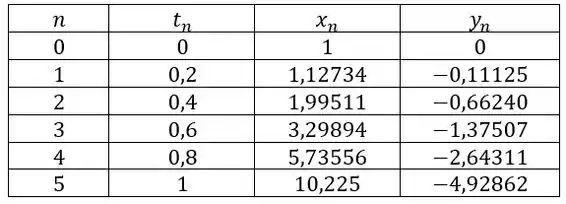
Resposta
Para e ;
Se fizer h = 0,05 e 0,025: x = 10,227, y = – 4,9294; estes resultados coincidem com a solução exata em cinco algarismos.