Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.5 - Ex. 1
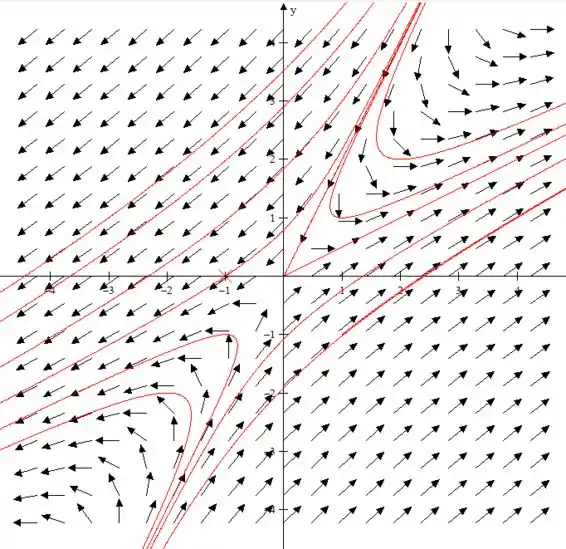
Em cada um dos problemas de a :
Encontre a solução geral do sistema de equações dado e descreva o comportamento das soluções quando
Desenhe um campo de direções e faça o gráfico de algumas trajetórias do sistema
Passo 1
A solução para esse tipo de sistemas de equações é do tipo:
Onde e
E essas letras aí podem ser encontradas fazendo:
E como não podemos considerar , pois aí seria a solução trivial então nós temos que fazer o determinante da matriz com (que são os autovalores):
Passo 2
Substituindo na equação matricial nós teremos:
E agora fazendo a multiplicação matricial:
E ambos os são linearmente dependentes de modo que:
Então o autovetor associado a será:
Pois se e teremos a igualdade na solução entendeu?
Então a primeira solução será:
Não se esquecer da constante.
Passo 3
Agora para teremos:
Então a multiplicação vetorial irá nos dar:
Onde e são linearmente dependentes em:
O que nos dá um autovetor de:
Logo a segunda solução será igual a:
Então a solução geral dessa equação diferencial será:
Passo 4
Desenhando algumas possíveis soluções nós teremos:
