Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.5 - Ex. 3

Em cada um dos problemas de 1 a 6 :

( a ) Encontre a solução geral do sistema de equações dado e descreva o comportamento das soluções quando t → ∞

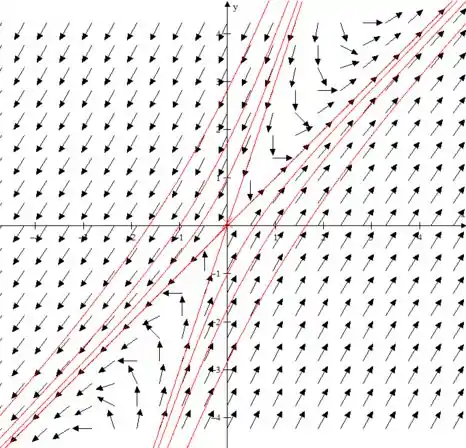
( b ) Desenhe um campo de direções e faça o gráfico de algumas trajetórias do sistema

x ' = 2 - 1 3 - 2 x

Passo 1

Aplicando o mesmo raciocínio nós temos que a solução do sistema de equações é:

x = c 1 ξ 1 e r 1 t + c 2 ξ 2 e r 2 t

Onde ξ 1 = ξ 1 1 ξ 2 1 e ξ 2 = ξ 1 2 ξ 2 2

E os autovalores ( r ) são encontrados ao fazer:

det ⁡ A - r I = 0

det ⁡ 2 - r - 1 3 - 2 - r = 0

Então fazendo o determinante temos:

2 - r - 2 - r - - 1 × 3 = 0

r 2 + - 2 + 2 r - 4 + 3 = 0

r 2 - 1 = 0

r = ± 1

Achamos os auto vetores agora vamos para os autovetores associados a eles

Passo 2

Começando pelo auto vetor de r = - 1 teremos:

2 - r - 1 3 - 2 - r ξ 1 1 ξ 2 1 = 0

2 + 1 - 1 3 - 2 + 1 ξ 1 1 ξ 2 1 = 0

3 - 1 3 - 1 ξ 1 ξ 2 = 0

Então conseguimos ver uma relação entre ξ 1 e ξ 2 igual a:

3 ξ 1 1 = ξ 2 1

Então o autovetor para r = - 1   será:

ξ 1 = ξ 1 1 ξ 2 1 = 1 3

Então a primeira solução será:

x 1 = c 1 1 3 e - t

Passo 3

Já o auto vetor associado ao auto valor r = 1 será:

2 - 1 - 1 3 - 2 - 1 ξ 1 2 ξ 2 2 = 0

1 - 1 3 - 3 ξ 1 2 ξ 2 2 = 0

O que nos dará uma relação entre ξ 1   e ξ 2 igual a:

ξ 1 2 = ξ 2 2

E o auto vetor tirado disso será:

ξ 2 = 1 1

Portanto a segunda solução será:

x 2 = c 2 1 1   e t

Onde a solução geral será:

x = c 1 1 3 e - t + c 2 1 1   e t

Passo 4

O diagrama de vetores e das famílias de solução dessa matriz serão dadas por:

Resposta

a )   x = c 1 1 3 e - t + c 2 1 1   e t

b )   I m a g e m   d o   p a s s o   4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O método de aproximações sucessivas (veja a Seção 2.8) também pode ser aplicado a sistemasde equações. Por exemplo, considere o problema de valor inicial x ' = A x , x 0 = x 0 Em que A e´uma matriz co
Em cada um dos Problemas 13 e 14, resolva o sistema de equações dado pelo método do Problema 19 da Seção 7.5. Suponha que t0. t x ' = 1 - 4 4 - 7 x
Em cada um dos problemas de 1 a 4:(a) Desenhe um campo de direções e esboce algumas trajetórias.(b) Descreva como as soluções se comportam quando t→∞ .(c) Encontre a solução geral do sistema de equaçõ
Em cada um dos problemas de 7 a 10:(a) Encontre a solução do problema de valor inicial dado.(b) Desenhe a trajetória da solução no plano x1x2 e desenhe, também, o gráfico de x1 em função de t. x ' = 1
Nos Problemas 5 e 6, encontre a solução geral do sistema de equações dado. x ' = 1 1 1 2 1 - 1 0 - 1 1 x