Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.5 - Ex. 8
Em cada um dos Problemas e :
Encontre a solução geral do sistema de equações dado
Desenhe um campo de direções e algumas das trajetórias. Em cada um desses, a matriz de coeficientes tem um autovalor nulo. Como resultado, o padrão das trajetórias é diferente dos padrões nos exemplos do texto
Passo 1
Se você leu a letra , você tomou aí o spoiler de que um dos auto valores é nulo, mas vamos confirmar ao encontrar os autovalores dessa matrizinha aí:
Fazendo a determinante nós teremos:
Então vemos que e , como respostas. Logo a solução geral ficará com a seguinte cara:
Passo 2
Então o auto vetor para será:
Onde
O que nos dá uma relação entre e igual a:
Portanto o autovetor será igual a:
Pois é a solução da igualdade. Logo a solução por esse autovetor será de:
Passo 3
E agora o autovetor causada por será de:
Onde
O que nos dá uma relação entre e igual a:
Então o autovetor será:
Logo a solução causada por esse autovalor será na ordem de:
Logo a solução geral será a soma das duas soluções e que será:
Passo 4
O campo de direções e algumas trajetórias possíveis nos dá a seguinte imagem abaixo:
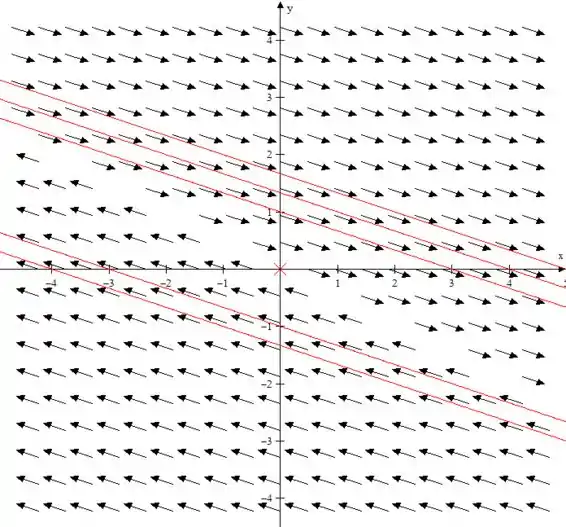
Ele segue um padrão bem mais reto que os anteriores (do 1 ao 6). Acho que dá para notar que as duas linhas tanto na 7 quanto na 8 são linearmente dependentes (se multiplicar por 2 na 7 e -2 na 8 a primeira linha você chega no resultado da segunda linha), isso faz com que um dos autovalores seja nulo, causando esse comportamento.