Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.6 - Ex. 4

Em cada um dos problemas de 1 a 6 :

( a ) Expresse a solução geral do sistema de equações dado como combinação e de funções reais

( b ) Desenhe, também um campo de direções, esboce algumas trajetórias e descreva o comportamento das soluções quando t → ∞

x ' = 2 - 5 / 2 9 / 5 - 1 x

Passo 1

Mesmo procedimento de sempre, vamos encontrar os autovalores dessa matriz:

det ⁡ 2 - r - 5 2 9 5 - 1 - r = 0

Fazendo essa determinante vamos encontrar:

2 - r - 1 - r + 9 2 = 0

r 2 + 1 - 2 r - 2 + 9 2 = 0

r 2 - r + 5 2 = 0

Resolvendo essa equação do segundo grau teremos os seguintes autovalores:

r 1 ; r 2 = 1 ± 1 - 4 × 5 2 2 = 1 2 ± 1 2 1 - 10 = 1 2 ± 3 i 2

Passo 2

Encontrando o autovetor para r = 1 2 + 3 i 2 nós teremos:

2 - 1 2 - 3 i 2 - 5 2 9 5 - 1 - 1 2 - 3 i 2 ξ 1 1 ξ 2 1 = 0

3 2 - 3 i 2 - 5 2 9 5 - 3 2 - 3 i 2 ξ 1 1 ξ 2 1 = 0

Fazendo a multiplicação vetorial nós vamos obter:

3 - 3 i ξ 1 1 - 5 ξ 2 1 = 0

E se fizermos ξ 1 1 = 5 e ξ 2 1 = 3 - 3 i nós solucionamos tanto o resultado da linha de cima quanto da de baixo. Logo o autovetor para o autovalor de r = 1 2 + 3 i 2 será:

ξ 1 = 5 3 - 3 i

Você pode sim pegar o outro auto valor ou até achar o autovetor com a segunda linha (dá no mesmo no final)

Nos dando uma solução igual a:

x 1 = 5 3 - 3 i e 1 2 + 3 i 2 t

x 1 = 5 3 - 3 i e t 2   e 3 i t 2 = 5 3 - 3 i e t 2   cos ⁡ 3 2 t + i   s e n 3 2 t

Então se arrumarmos a casa (separar a parte real da imaginária) nós teremos:

x 1 = 5 cos ⁡ 3 2 t 3 cos ⁡ 3 2 + 3 s e n 3 2 t e t 2 + i 5 s e n 3 2 t 3 s e n 3 2 t - 3 cos ⁡ 3 t 2 e t 2

Portanto a solução geral será:

x = c 1 5 cos ⁡ 3 2 t 3 cos ⁡ 3 2 + 3 s e n 3 2 t e t 2 + c 2 5 s e n 3 2 t 3 s e n 3 2 t - 3 cos ⁡ 3 t 2 e t 2

Passo 3

Desenhando o campo de direções desse sistema teremos:

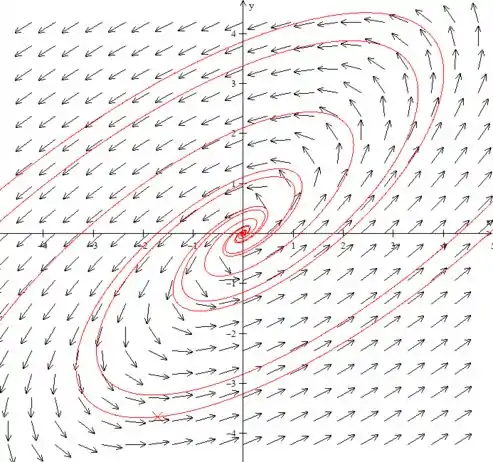
Ambos os módulos de x ( x 1 e x 2 ) tendem a ir para um número muito alto quando t → ∞

Resposta

a )   x = c 1 5 cos ⁡ 3 2 t 3 cos ⁡ 3 2 + 3 s e n 3 2 t e t 2 + c 2 5 s e n 3 2 t 3 s e n 3 2 t - 3 cos ⁡ 3 t 2 e t 2

b ) I m a g e m   d o   P a s s o   3  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

28- Uma massa m em uma mola com constante k satisfaz a equação diferencial (veja a Seção 3.7 ) m v ' ' + k v = 0 Em que v ( t ) é o deslocamento da massa no instante t a partir de sua posição de equil
Em cada um dos problemas de 13 a 20, a matriz de coeficientes contém um parâmetro α. Em cada um desses problemas: (a) Determine os autovalores em função de α. (b) Encontre o valor ou valores críticos
Resolva o problema de valor inicial x ' = - 1 - 4 1 - 1 x , x 0 = 3 1 usando a matriz fundamental Φ ( t ) encontrada no Problema 6.
Resolva o problema de valor inicial x ' = 2 - 1 3 - 2 x , x 0 = 2 - 1 usando a matriz fundamental Φ ( t ) encontrada no Problema 3.
Mostre que Φ t =Ψ t Ψ - 1 ( t 0 ) , em que Φ ( t ) e Ψ ( t ) são como definidas nesta seção.