Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 5.10 - Ex. 1d
Em cada um dos seguintes casos, verificar se o Teorema do Valor Médio se aplica. Em caso afirmativo, achar um número em , tal que
Interpretar geometricamente.
(d) ; .
Passo 1
Bom, pessoal, para sabermos se o Teorema do Valor Médio se aplica, precisamos saber se a é contínua no intervalo dado. No intervalo , temos que a função é contínua e derivável, pois é do tipo polinomial.
Assim, vamos calcular !
Vamos substituir os valores aqui. Como e .
Passo 2
Interpretação geométrica: a figura que segue mostra que a reta tangente no ponto , representada pela cor azul é paralela à reta secante que passa nos pontos e , representada na cor verde.
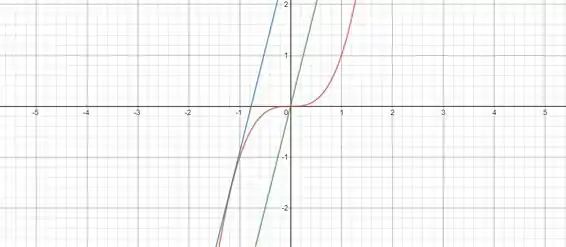
Resposta
O número é igual a:
Exercícios de Livros Relacionados
Use o grafico dado no exerciico 7 para etsimar os valores de c que satisfaçam àconclusao do teorema do valor medio pra [ 1,7 ]
Seja f x = x - 1 - 2 . Mostre que f 0 = f 2 , mas não existe c em 0,2 tal que f ' c = 0 . Por que isso não contradiz o Teorema de Rolle?
Verifique que a função satisfaz as três hipóteses do Teorema de Rolle sobre o intervalo dado. Então encontre todos os numero c que satisfazem a conclusão do teorema de Rolle. f x = x x + 6 , [ - 6,0 ]
Seja f x = x + 1 x - 1 . Mostre que não existe c tal que f ( 2 ) - f 0 = f ' ( c ) ( 2 - 0 ) . Por que isso não contradiz o Teorema do Valor Médio?
Às 2 horas da tarde o velocímetro de um carro mostrava 30m i / h , e às 2 h 10 mostrava 50m i / h . Mostre que em algum instante entre 2 h e 2 h 10 a aceleração é exatamente 120 m i / h 2 .