Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.11 - Ex. 28
Para cada uma das seguintes funções () dê uma definição como aquelas em (), () esboce o gráfico e () encontre uma fórmula similar à Equação .
(a)
(b)
(c)
Passo 1
Fala meus queridos... nessa questão nós temos 3 funções hiperbólicas inversas que são:
E nós vamos ter que fazer 3 coisas com essas funções.
1. Desinverter a função, isso é, se temos que é igual a inversa de , então temos que é igual a função original de .
2. Esboçar o gráfico da inversa. Para isso, vamos usar um software de gráficos.
3. Encontrar uma fórmula para . Para isso, vamos usar algumas relações para nos ajudar:
,
,
E
Passo 2
Na letra a), temos:
()
()
()
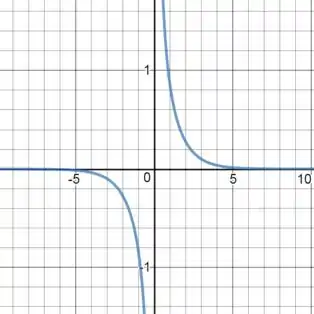
Agora usando uma relação hiperbólica, temos que:
Substituindo o que encontramos anteriormente:
Então, pelo exercício que nos diz que
Trocando os lados e aplicando .
Logo:
Passo 3
Item b:
()
()
()
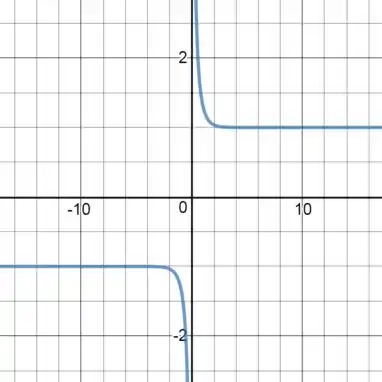
Aplicando dos dois lados.
Passo 4
Item c:
()
()
()
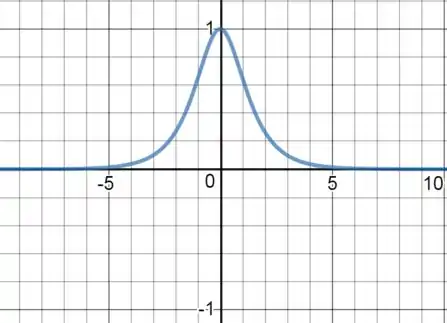
Usando uma relação hiperbólica, temos:
Então, pelo exercício que nos diz que
Logo:
Resposta
Resolução nos Passos.