Represente graficamente as equações dos Exercícios 9-58 seguindo os passos do procedimento para construção de gráficos da página 237. Inclua as coordenadas de quaisquer pontos extremos e absolutos locais e pontos de inflexão.

40-

Vamos encontrar nossos pontos críticos analisando

O único valor elevado ao cubo que da 1 é o próprio 1.

Note que tanto na própria função como na sua primeira derivada temos um parcela inversa , ela nos dá nossa assíntota vertical onde se .

Então temos duas funções diferentes uma positiva outra negativa.

Agora analisando , podemos achar os pontos de mínimo e máximo e ponto de inflexão :

Testando para :

Logo para , temos mínimo local , concavidade para cima:

Inflexão:

Temos x= como nosso valor de inflexão

Como já encontramos a assíntota vertical da função, vamos calcular agora se temos assíntotas horizontais:

Para x tendendo a infinito:

Podemos aplicar L’Hopital por que temos indeterminação :

O que nos dá :

Agora para tendendo a menos infinito:

Podemos aplicar L’Hopital por que temos indeterminação :

O que nos dá :

Pois eleva-se ao quadrado, mudando o sinal.

Precisamos também fazer o limite em relação a assíntota vertical :

Fazendo tender a zero indo da direita para a esquerda:

Fazendo tender a zero indo da esquerda para a direita:

Como sabemos o comportamento da nossa função vamos organizar nossos intervalos :

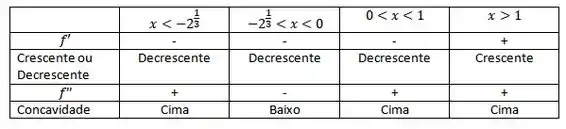
Valores de x para o teste: -2,-1,0.5 e 2