Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.11 - Ex. 22
(a) Use os gráficos de , e das Figuras para fazer os gráficos de , e .
(b) Verifique os gráficos que você esboçou no parte (a) usando uma ferramenta gráfica para produzi-los.
Passo 1
Oieeee, bora resolver mais uma comigo?
Para fazer os gráficos das funções , e , podemos utilizar as seguintes definições:
Vamos usar as informações dos gráficos das funções , e para plotar os gráficos de , e .
(a) Com base nas definições acima e nos gráficos dados, podemos plotar os gráficos das funções:
é a inversa de , então onde é próximo de zero, será grande. O gráfico de mostra que é próximo de zero onde é próximo de zero, então será grande perto de
é a inversa de então onde é próximo de zero, será grande. O gráfico de mostra que é próximo de zero onde é grande (à medida que se aproxima do infinito negativo ou positivo), então será grande para valores grandes de
é a inversa de , então onde é próximo de zero, será grande. O gráfico de mostra que é próximo de zero onde é grande (à medida que se aproxima do infinito negativo ou positivo), então será grande para valores grandes de
Passo 2
Para a cossecante hiperbólica:
Se o gráfico do seno hiperbólico é:
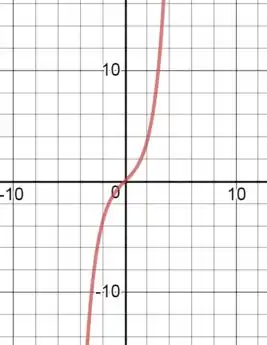
E como
Então, vemos que a pedida que os valores de vão para o infinito, os valores de convergem para zero, e à medida em que os valores de vão para zero, por valores diferentes de zero, os valores de vão para o infinito com mesmo sinal de .
Ou seja, temos o gráfico:
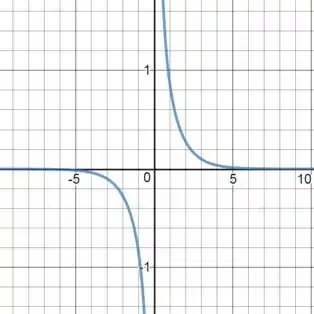
Passo 3
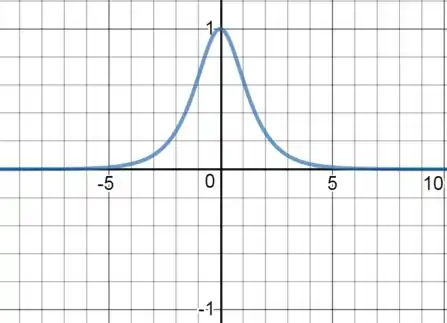
Para a secante hiperbólica:
Se o gráfico do cosseno hiperbólico é:
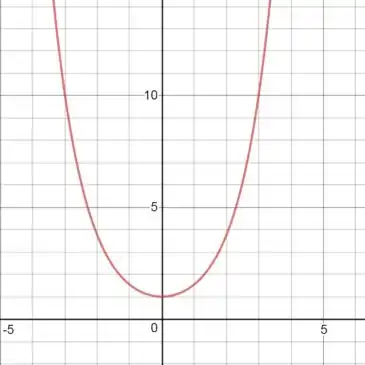
E como
Então, vemos que a pedida que os valores de vão para o infinito, os valores de convergem para zero, e à medida em que os valores de vão para zero, por valores diferentes de zero, os valores de vão para o infinito com mesmo sinal de .
Ou seja, temos o gráfico:
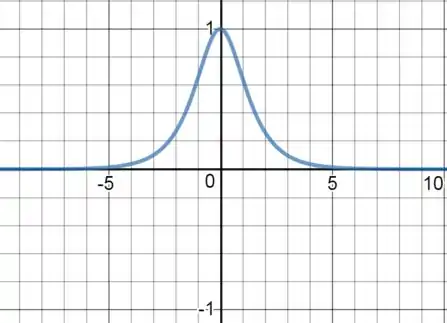
Passo 4
Ou seja, temos o gráfico:
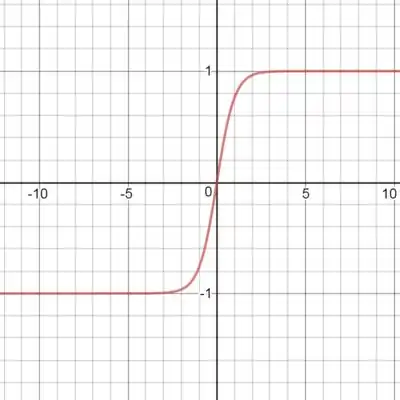
Para a cotangente hiperbólica:
Se o gráfico da tangente hiperbólica é:
E como
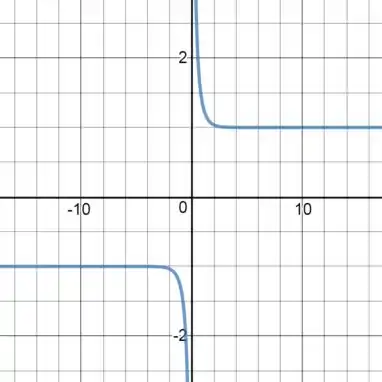
Então, vemos que a pedida que os valores de vão para o infinito, os valores de convergem para zero, e à medida em que os valores de vão para zero, por valores diferentes de zero, os valores de vão para o infinito com mesmo sinal de .
Ou seja, temos o gráfico:
Resposta
Vide o passo a passo.