Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.Revisão - Ex. 55
Uma caixa aberta com uma base quadrada deve ter um volume de . Ache as dimensões da caixa que posso ser fabricada com um mínimo de material.
Passo 1
Seja a caixa como da figura abaixo:
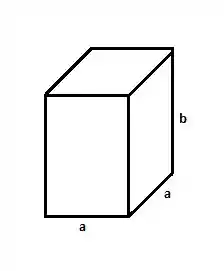
Onde os lados da base medem e a altura mede . O volume desta caixa é dado por:
Como, por hipótese, a caixa tem volume de temos:
Note que, como e são medidas dos lados da caixa temos e .
Passo 2
Vamos determinar a área total da caixa.
Área da base: ;
Área lateral: ;
Área total: .
De (1):
Como a equação da área só depende da variável podemos reescrever:
Passo 3
Derivando temos:
Como existe para todo , temos que os pontos críticos de ocorrem quando . Assim:
Passo 4
Vamos fazer o estudo de sinal da derivada em torno de . Assim:
Se temos , logo é decrescente;
Se temos , logo é crescente.
Logo, em temos um ponto de mínimo da função . Substituindo em (1) temos:
Resposta
Portanto, uma caixa aberta com uma base quadrada com volume de deve ter de comprimento do lado da base e de altura para gastar o mínimo de material.