Uma horta de ervilhas retangular com será cercada e dividida em duas parte iguais por outra cerca paralela a um dos lados. Quais as dimensões do retângulo externo que exigirão a menor quantidade total de cerca? Quantos metros de cerca serão necessários?
Passo 1
A nossa situação é a seguinte:
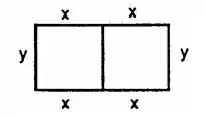
O total de cerca vai ser:
Aqui entra por que, além das cercas de comprimento laterais, também tem uma no meio de comprimento que divide os dois pedaços, beleza? 😉
Contando apenas os lados do retângulo.
Além disso, ele deu a área, vamos ter:
Assim,
O total de cerva vai ser:
Onde precisa ser maior que
Ele não pode ser zero porque temos o no denominador
Passo 2
Para acharmos o valor de mínimo ou máximo, temos que comparar o valor da função nos pontos críticos e nos extremos do intervalo.
Começando por achar os pontos críticos:
Colocando a fração como potência:
Derivando:
Fazendo isso igual a
Além disso, vamos ter o ponto crítico quando , porque a derivada não existe nesse caso.
Mas de todos esses valores, apenas o serve para nós.
Passo 3
Vamos achar o valor da função nos pontos críticos e extremos do intervalo:
Ele só deu a limitação em certo? Quer dizer que a outra limitação é o infinito.
O menor dos valores é quando
Entao o retângulo tem dimensões:
E comprimento mínimo
Resposta
Dimensão
Comprimento mínimo: