Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 11
Você está preparando um pôster retangular que deverá conter de material impresso, com margens superior e inferir de Cada uma e margens à direita e À esquerda de cada uma . Que dimensões gerais minimizarão a quantidade de papel a ser utilizada?
Passo 1
Vamos chamar de e o tamanho da folha d eimpressão do poster.
Dessa forma, vamos ter a seguinte figura com a margem.
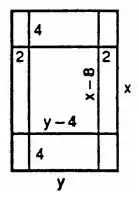
A parte impressa vai ser o tamanho da folha menos a margem, que vai ser um retângulo de lados e . A área do papel vai ser:
Ele deu a área da parte impressa, então vamos ter:
Assim,
A área da folha vai ser:
Onde precisa ser maior que e o precisa ser maior que , que são as margens.
Como temos uma relação dos dois, não precisamos nos preocupar com ambos os intervalos, vamos pegar só o de já que nossa função da área so ficou com
Passo 2
Para acharmos o valor de mínimo ou máximo, temos que comparar o valor da função nos pontos críticos e nos extremos do intervalo.
Começando por achar os pontos críticos:
Para isso, vamos derivar usando a regra do quociente no segundo termo:
Fazendo isso igual a
Cortando o dos dois lados
Multiplicnado cruzado:
Vamos ter:
Ou
Como precisa ser maior que , vamos pegar apenas o .
Passo 3
Vamos achar o valor da função nos pontos críticos e extremos do intervalo:
Ele só deu a limitação em certo? Quer dizer que a outra limitação é o infinito.
Nesse valor de indo para infinito, o segundo termo, o da fração vai para , so que o já deixa tudo infinito, então ele vai para infinito mesmo.
O menor dos valores é quando
Então vamos ter
E
Resposta
Letra