Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 63
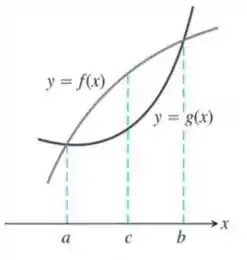
Sejam e as funções deriváveis traçadas aqui. O ponto é onde a distância vertical entre as curvas é máxima. Há algo especial sobre as tangentes às duas curvas em ? Justifique sua resposta.
Passo 1
Nos foi dado que o ponto é um ponto onde a distância na vertical entre as curvas é máxima. Desejamos saber se há algo de especial com relação as tangentes, que é a interpretação geométrica da derivada, nesse ponto.
Passo 2
Chamemos a distância entra as duas curvas de . Assim,
Sabemos que a derivada da soma/subtração é a soma/subtração das derivadas. Dessa forma podemos fazer
O máximo valor de ocorrerá exatamente no ponto como foi enunciado na questão, dessa forma é também um ponto crítico de , então,
Como a derivada geometricamente representa a inclinação da reta tangente em um ponto, no nosso caso, para o ponto teremos que as tangentes das duas curvas serão paralelas, pois apresentam mesmo coeficiente angular.
Resposta
Ei, a resposta está no passo a passo :)