Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.1 - Ex. 9
Com uma calculadora programável (ou um computador), é possível calcular as expressões para a soma das áreas de retângulos aproximantes, mesmo para valores grandes de , usando . (Numa use o comando numa Casio use , numa HP ou no BASIC use um laço FOR-NEXT.)
Calcule a soma das áreas dos retângulos aproximantes usando subintervalos iguais e extremidades direitas para . Então, conjecture o valor exato da área.
A região sob de até .
Passo 1
Fala aí, tudo certinho com você?
Bom, essa quatão fala pra gente que com uma calculadora programável (ou um computador), é possível calcular as expressões para a soma das áreas de retângulos aproximantes, mesmo para valores grandes de , usando .
(Numa use o comando numa Casio use , numa HP ou no BASIC use um laço FOR-NEXT.)
E pede pra gente calcular a soma das áreas dos retângulos aproximantes usando subintervalos iguais e extremidades direitas para
E então, conjecturar o valor exato da área.
A região sob
de até .
E para isso, colocaremos um algoritmo ordenado pela sequência de operações para calcularmos as somas.
Vem comigo que te mostro tudo direitinho no passo a passo.
Passo 2
1º Colocamos
(no lugar de podemos ter também ou dependendo de qual soma estivermos calculando),
e
Passo 3
2º Devemos repetir os passos 2a e 2b em sequência:
a) Adicionamos a soma.
b) Adicionamos a .
Ao final do processo, é igual a resposta que estamos procurando. Nós encontramos que:
Isso demonstra que a área exata é .
Passo 4
Abaixo temos o programa
e vem de uma calculadora Plus.
Para generalizar o programa, nós temos valores de entrada (em vez dos atribuídos) para e
Além disso, a função
é chamada de
nos possibilitando avaliar qualquer soma apenas mudando e executando o programa:
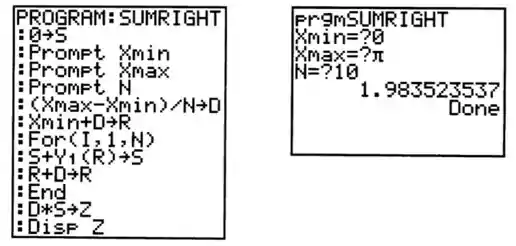
Resposta
O valor exato da área é .