Calcular a área da superfície do tetraedro cujas faces são partes dos planos , , e

Novamente temos um exercício desafiador. Sim acho que esse vai dar um trabalho.

Vamos obviamente trabalhar cada superfície separada definindo seus limites de integração e ao fim integrar todas.

Começando com a superfície que está no plano .

Devemos encontrar como os outros planos cruzam com esse em específico.

Já sabemos que o plano nos indica que estamos trabalhando, por enquanto, com o plano na qual .

Agora analisando o plano , em temos

E com o plano , em temos =

Assim, se visualizando a superfície que forma no plano , teremos

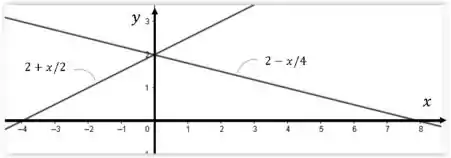
Na qual a superfície que nos interessa é essa cercada pelas nossas retas indicadas acima.

Vamos confirmar os valores encontrados.

Quando

Para a reta , quando e para reta , quando .

Nossa integral pode ser escrita como

Que não é uma integral difícil de resolver

E por fim

Vamos para a próxima superfície?

Vamos tomar o plano . Quando o mesmo cruza com o plano , temos que, ou ficamos com a parte onde ou a parte onde . Isso vamos saber analisando como os outros planos cruzam com o plano .

Agora analisando o plano , em temos

E com o plano , em temos =

Para a reta quando e quando .

Para a reta quando e quando .

Já sabemos que as retas se encontram em quando , pois as duas retas apresentaram o mesmo valor. Assim temos

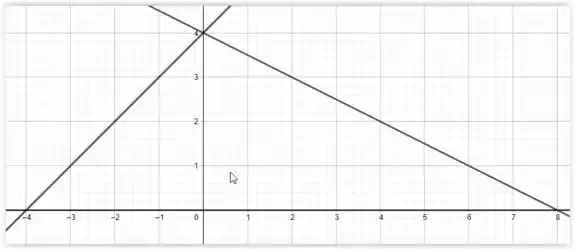
Que é nosso gráfico no plano . Da mesma forma que a superfície anterior, teremos que nossa integral é escrita em duas partes.

Que também não é uma integral difícil de resolver

E por fim

Agora Vamos analisar a próxima superfície no plano

Primeiro vamos calcular o fator de integração, ou seja, tome que

Assim teremos que nossas derivadas direcionais são:

E

Assim ficamos com

Onde agora precisamos descobrir os limites de integração. Devemos lembrar que nossos limites estão relacionados com a projeção que nossa superfície faz no nosso plano , assim vamos tomar quando , ficando com

Que se a gente observar bem a primeira Fig, tínhamos que essa era a equação que esse plano produzia no plano . Então teremos que nossa integral pode ser escrita como

Resolvendo, temos

Seguindo a mesma ideia acima para o outro plano, temos que

Calculando as derivadas direcionais, temos

E

Assim o fator de integração será

A reta que intercepta o plano é

Que é vista na FIg 1.

Assim nossa integral será

Que será

Assim por fim, finalmente teremos que