Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 9.3 - Ex. 13

Seja K o conjunto do plano x y limitado pelas curvas (em coordenadas polares) ρ = t g   θ , 0 < θ < π 2 ,   e   θ = π 4 . Calcule a área da superfície z = x y , x , y ∈ K .

Passo 1

Pra a gente ter uma ideia do intervalo, vamos ver a figura:

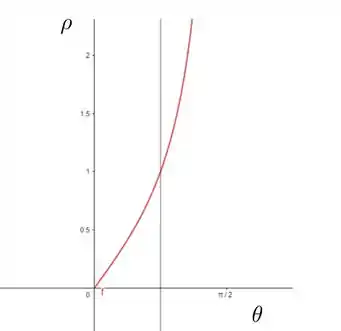
Vemos então que o intervalo de θ se limita a 0 < θ < π 4 . E que o intervalo de ρ é:

0 < ρ < t g   θ .

A gente sabe que pra calcular área de superfície, nós usamos a fórmula:

A = ∬ K 1 + ∂ z ∂ x 2 + ∂ z ∂ y 2 d x d y

Vamos trazer isso pro nosso caso então...

Passo 2

As derivadas parciais da superfície z = x y é:

∂ z ∂ x = y     e     ∂ z ∂ y = x

Então na fórmula teríamos:

A = ∬ K 1 + x 2 + y 2   d x d y

Como a gente tá lidando com coordenadas polares, e sabemos que:

x = ρ cos ⁡ θ y = ρ s e n   θ ,       x 2 + y 2 = ρ 2 ;           d x d y = ρ d ρ d θ

E então, usando os intervalos encontrados anteriormente e essa relação, podemos escrever nossa integral da área:

A = ∫ 0 π 4 ∫ 0 t g   θ 1 + ρ 2   ρ d ρ d θ

Beleza, só calcular agora😊

Passo 3

Resolvendo a integral:

Vamos começar com uma substituição simples: u = 1 + ρ 2 → d u = 2 ρ .

A = ∫ 0 π / 4 1 2 ∫ u   d u

A = 1 2 ∫ 0 π 4 2 3 u 3 2 d θ

(voltamos para a variável ρ )  

A = 1 2 ∫ 0 π 4 2 3 [ 1 + ρ 2 3 2 ]   0 t g   θ d θ

A = 1 2 ⋅ 2 3 ∫ 0 π 4 1 + t g 2 θ 3 2 - 1   d θ

Usando a relação 1 + t g 2 θ = sec 2 ⁡ θ , ficamos com:

A = 1 3 ∫ 0 π / 4 sec 3 ⁡ θ - 1   d θ

(Aqui a gente usa aquelas fórmulas de redução das funções trigonométricas, mas pode fazer por partes também)

Vamos ter:

A = 1 3 1 2 sec ⁡ θ t g   θ + 1 2 ln ⁡ sec ⁡ θ + t g   θ - θ 0 π 4

Aplicando os intervalos agora achamos a área:

A = 1 3 2 2 + ln ⁡ 2 + 1 2 - π 12

E agora acabou😉

Resposta

A = 1 3 2 2 + ln ⁡ 2 + 1 2 - π 12

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a área das seguintes superfícies: Superfície do cilindro x 2 + y 2 = 2 x limitado pelos planos z = 0 e o cone z = x 2 + y 2 .
Calcule a área das seguintes superfíciesg) Superfície da esfera de raio a centrada na origem limitada por dois planos paralelos e dois meridianos, sabendo-se que o ângulo entre os meridianos é α e a d
Considere γ o arco da parábola z = 3 - y 2 no plano y z compreendido entre as semi-retas z = z = 2 y e z = 11 2 y , com y ≥ 0 . Seja S a superfície obtida girando-se γ em torno do eixo z . Pede-se:Uma
Calcule a área das seguintes superfícies. d) Superfície da esfera x 2 + y 2 + z 2 = 12 que não está no interior do paraboloide z = x 2 + y 2 .
∬_S (x^2 + y^2) d S , onde S é a esfera x^2 + y^2 + z^2 = a^2 .