Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 9.2 - Ex. 26

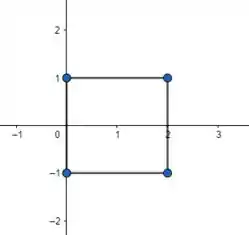
Calcular o centro de massa de um arame com forma de um quadrado de vértices 0 , - 1 ,   2 , - 1 ,   2,1   e   ( 0,1 ) , sabendo que a densidade no ponto ( x , y ) é proporcional ao quadrado da distância desse ponto até a origem.

Passo 1

A densidade é dada por x 2 + y 2 .

A gente vai ter que dividir essa região, porque ela é formada por 4 retas.

Passo 2

Vamos calcular da primeira reta. A que passa por 0 , - 1   e   ( 2 , - 1 ) :

A reta é:

r : x = 2 t y = - 1 ,   t ∈   [ 0,1 ]

A derivada:

r ' = ( 2,0 )

A norma:

d s = 2

A massa então:

M = ∫ 0 1 4 t 2 + 1 2 d t

M = ∫ 0 1 8 t 2 + 2   d t

8 t 3 3 + 2 t 0 1 = 8 3 + 2 = 14 3

E aí o centro de massa é:

x - = 1 14 3 ∫ 0 1 2 t 4 t 2 + 1 2 d t

= 3 14 ∫ 0 1 16 t 3 + 4 t   d t

= 3 14 16 t 4 4 + 4 t 2 2 0 1

= 3 14 4 + 2

= 9 7

E a coordenada y ...

y - = 1 14 3 ∫ 0 1 - 1 4 t 2 + 1 2 d t

y - = 3 14 ∫ 0 1 - 8 t 2 - 2   d t

= 3 14 - 8 t 3 3 - 2 t 0 1

= 3 14 - 8 3 - 2 = 3 14 - 14 3 = - 1

Passo 3

Vamos para a reta que liga 2 , - 1   a   ( 2,1 ) :

r : x = 2 y = - 1 + 2 t ,   t ∈ [ 0,1 ]

A derivada aqui é r ' = ( 0,2 ) e a norma é 2 .

Vamos montar a integral da massa:

M = ∫ 0 1 ( 2 2 + - 1 + 2 t 2 2 d t

= ∫ 0 1 4 + 1 - 4 t + 4 t 2 2 d t

= ∫ 0 1 10 - 8 t + 8 t 2 d t

= 10   t - 8 t 2 2 + 8 t 3 3 0 1

  M = 10 - 4 + 8 3 = 2 6 3

O centro de massa agora:

x - = 1 26 3 ∫ 0 1 2 10 - 8 t + 8 t 2 d t

= 3 2 6 20 t - 16 t 2 2 + 16 t 3 3 0 1  

= 3 2 6 20 - 8 + 16 3

= 3 2 6 52 3 = 2

A coordenada y :

1 8 ∫ 0 1 - 1 + 2 t 10 - 8 t + 8 t 2 d t

1 8 ∫ 0 1 - 10 + 8 t - 8 t 2 + 20 t - 16 t 2 + 16 t 3   d t

1 8 - 10 t + 28 t 2 2 - 24 t 3 3 + 16 t 4 4 0 1

1 8 - 10 + 14 - 8 + 4 = 0

Passo 4

Agora vamos para a reta que vai de 2,1   a   ( 0,1 ) .

r :   x = 2 - 2 t y = 1 ,   t ∈ [ 0,1 ]

A norma que é o nosso d s é 2 .

Montando a integral da massa então:

M = ∫ 0 1 2 - 2 t 2 + 1 2 2 d t

∫ 0 1 ( ( 4 - 8 t + 4 t 2 ) + 1 ) 2 d t

= ∫ 0 1 10 - 16 t + 8 t 2 d t

= 10 t - 16 t 2 2 + 8 t 3 3 0 1

= 10 - 8 + 8 3 = 14 3

O centro de massa agora:

x - = 3 14 ∫ 0 1 2 - 2 t 10 - 16 t + 8 t 2 d t

= 3 14 ∫ 0 1 20 - 32 t + 16 t 2 - 20 t + 32 t 2 - 16 t 3 d t

= 3 14 - 16 t 4 4 + 48 t 3 3 - 5 2 t 2 2 + 20 t 0 1

= 3 14 - 4 + 16 - 26 + 2 0

= 3 14 6 = 18 14 = 9 7

A coordenada y ...

y - = 3 14 ∫ 0 1 1 10 - 16 t + 8 t 2 d t

= 3 14 14 3 = 1

Passo 5

Vamos para a última reta agora, que vai de 0,1 a   ( 0 , - 1 ) :

r : x = 0 y = 1 - 2 t ,   t ∈ [ 0,1 ]

E a norma aqui é 2 também.

Montando a integral da massa:

M = ∫ 0 1 1 - 2 t 2 2 d t

= ∫ 0 1 1 - 4 t + 4 t 2 2 d t

= ∫ 0 1 2 - 8 t + 8 t 2 d t

= 2 t - 8 t 2 2 + 8 t 3 3 0 1

= 2 - 4 + 8 3

= 2 3

O centro de massa...

x - = 3 2 ∫ 0 1 0 2 - 8 t + 8 t 2 d t

= 0

A coordenada y ...

y - = 3 2 ∫ 0 1 1 - 2 t 2 - 8 t + 8 t 2 d t

= 3 2 ∫ 0 1 2 - 8 t + 8 t 2 - 4 t + 16 t 2 - 16 t 3 d t

= 3 2 - 16 t 4 4 + 24 t 3 3 - 12 t 2 2 + 2 t 0 1

= 3 2 - 4 + 8 - 6 + 2

= 0

Passo 6

Somando tudo agora, temos as coordenadas do centro de massa:

x - = 9 7 + 2 + 9 7 = 32 7

y - =   - 1 + 1 + 0 + 0 = 0

C m = 32 7 ,   0

Resposta

C m = 32 7 ,   0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se F é o campo vetorial do Exemplo 5, mostre que ∫ C F ⋅ d r = 0 para todo caminho fechado simples que não passe pela origem e nem a circunde. F x , y = - yi + xj x 2 + y 2
Use o Exercício 22 para encontrar o centroide de um quarto de uma região circular de raio a .
Uma lâmina plana com densidade constante ρ x ,y = ρ ocupa uma região do plano x y limitada por um caminho fechado simples C . Mostre que seus momentos de inércia em relação aos eixos são I x = - ρ 3 ∮
Seja D a região limitada por um caminho fechado simples C no plano x y . Utilize o Teorema de Green para demonstrar que as coordenadas do centroide ( x - ,y - ) de D são x - = 1 2 A ∮ C x 2d y y - = -
Utilize o Exercício 25 para achar o momento de inércia de um círculo de raio a com densidade constante em relação a um diâmetro (compare com o Exemplo 4 da Seção 15.5)