Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 5.10 - Ex. 68
Calcular as dimensões de um retângulo de área máxima inscrito numa semicircunferência de raio 2.
Passo 1
Beleza galera, vamos olhar o que está acontecendo:
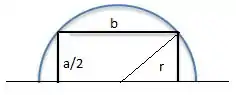
A diagonal da metade do retângulo é dada por:
Neste caso nós temos um problema de otimização restrita, ou seja, queremos encontrar o valor máximo para a área, mas sabendo que
Elevando ambos os lados ao quadrado elembrando que :
Então, nós teremos o seguinte problema de otimização:
Passo 2
Colocando na fórmula de Lagrange:
Derivando L em relação às variáveis a e b e igualando as derivadas a zero:
Igualando as duas primeiras equações nós achamos:
Como estamos nos tratando de medidas, teremos o valor positivo.
Colocando na última equação:
Achando a:
As dimensões do retângulo então serão .
E fim galerinhaa!
Resposta
Exercícios de Livros Relacionados
Determine os valores extremos de f sujeita a ambas as restrições. f x , y , z = x 2 + y 2 + z 2 , x - y = 1 , y 2 - z 2 = 1
Encontre o valor mínimo de f x , y , z = x 2 + 2 y 2 + 3 z 2 sujeito a restrição x + 2 y + 3 z = 10 . Mostre que f não tem valor máximo com essa restrição.
Cada um desses problemas de valor extremo possui uma solução com um valor máximo e um valor mínimo. Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita
O método dos multiplicadores de Lagrange assume que os valores extremos existem, mas esse nem sempre é o caso. Mostre que o problema de encontrar o valor mínimo de f x , y = x 2 + y 2 sujeito a restri
Utilize os multiplicadores de Lagrange para dar uma solução alternativa aos exercícios da Seção 14.7 indicados.Exercício 41