Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 9.4 - Ex. 31
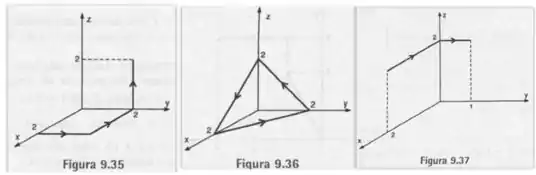
Calcular a integral ao longo de , que é mostrado nas figuras , e .
Passo 1
O que vamos fazer em cada item é, identificar os pontos e o caminho a ser seguindo. Para cada segmento devemos fazer parametrizações diferentes. Uma vez que a gente conhece as parametrizações, podemos começar a resolver nossa integral.
Passo 2
Para a Fig. 9-35, temos o seguinte caminho
As setinhas indicam quantas parametrizações precisaremos.
De
De
De
Onde todos o varia de a .
Assim fazemos agora que para cada linha temos:
Agora ainda para a Fig. 9-35 vamos resolver nossa integral
Passo 3
Para a Fig. 9-36, temos o seguinte caminho
As setinhas indicam quantas parametrizações precisaremos.
De
De
De
Onde todos o varia de a .
Assim fazemos agora que para cada linha temos:
Agora ainda para a Fig. 9-36 vamos resolver nossa integral
Passo 4
Para a Fig. 9-36, temos o seguinte caminho
As setinhas indicam quantas parametrizações precisaremos.
De
De
Onde todos o varia de a .
Assim fazemos agora que para cada linha temos:
Agora ainda para a Fig. 9-37 vamos resolver nossa integral