Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 9.4 - Ex. 26c
Calcular a integral , onde C é:
c) A poligonal de (0,0) a (0,1) a (-1,-2).
Passo 1
Bora continuar!
Vamos desenhar os pontos para ficar mais claro, certo?
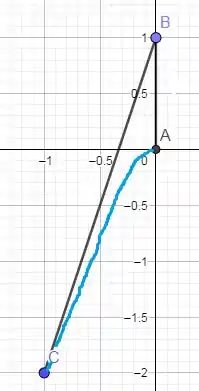
Então, a nossa poligonal irá unir o ponto A ao C. Para calcular a integral de linha, nós poderemos a equação da reta de BC, que apresenta os mesmos intervalos quanto à variável que nos interessa, o x.
Substituindo os pontos B e C na equação da reta:
Então a equação da reta é:
E o intervalo será:
Substituindo na integral:
Passo 2
Vamos resolver cada integral separadamente:
Resolvendo por partes:
Então:
Aplicando o intervalo:
Concluindo que:
Resolvendo a segunda:
Aplicando o intervalo:
Aplicando na integral do Passo 1:
Como a reta está no sentido que consideramos anti-horário:
E acabamos !!
Resposta
Exercícios de Livros Relacionados
Faça uma correspondência entre as funções f e os desenhos de seus campos vetoriais gradientes (rotulados de I - I V ). Justifique suas escolhas. f x ,y = x 2 + y 2
Faça uma correspondência entre as funções f e os desenhos de seus campos vetoriais gradientes (rotulados de I - I V ). Justifique suas escolhas. f x ,y = x ( x + y )
Faça uma correspondência entre as funções f e os desenhos de seus campos vetoriais gradientes (rotulados de I - I V ). Justifique suas escolhas. f x ,y = x + y 2
No instante t = 1 , uma partícula está localizada na posição 1 ,3 . Se ela se move em um campo de velocidade F x , y = x y - 2 ,y 2 - 10 encontre sua posição aproximada no instante t = 1,05 .
(a) Esboce o campo vetorial F x ,y = i + xj e algumas linhas de escoamento. Qual é o formato que essas linhas de escoamento parecem ter?(b) Se as equações paramétricas das linhas de escoamento são x =