Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 8.7 - Ex. 23d

Calcular as seguintes integrais:

int_(- 1)^1 int_(- sqrt(1 - x^2))^(sqrt(1 - x^2)) int_((x^2 + y^2)^2)^1 x^2 d z . d y . d x

Passo 1

Bora começar?!

Então galera, pela primeira integral nós vemos que o z vai de (x^2 + y^2)^2 até 1.

Então nosso desenho ficará assim:

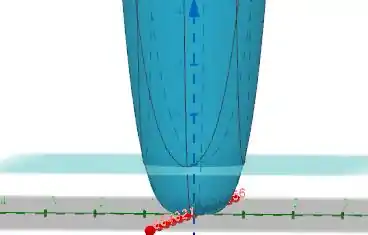
Neste caso é legal nós usarmos coordenadas cilíndricas, onde:

x^2 + y^2 = r^2

z = (r^2)^2 = r^4

Então z irá:

r^4 <= z <= 1

O maior raio será obtido quando z equivale a um, não é?

1 = r^4

r = +- 1

Shooow!! Já temos o intervalo de r:

0 <= r <= 1

Legal, agora só precisamos de theta .

O theta é o ângulo que o ponto pode fazer com o eixo x, no círculo esse ângulo vai de 0 até 360°, então:

0 <= theta <= 2 pi

Passo 2

Agora que já sabemos os intervalos de integração, podemos usar a definição (4) para mudar as variáveis de integração:

int_(- 1)^1 int_(- sqrt(1 - x^2))^(sqrt(1 - x^2)) int_((x^2 + y^2)^2)^1 x^2 d z . d y . d x

Lembrando que:

x = r . cos ( theta )

Então:

= int_0^(2 pi) int_0^1 int_(r^4)^1 ( r^2 . cos^2 ( theta ) ) r d z . d r . d theta

= int_0^(2 pi) int_0^1 int_(r^4)^1 ( r^3 ) d z . d r . cos^2 ( theta ) . d theta

Resolvendo:

int_(r^4)^1 ( r^3 ) d z = r^3 z = r^3 ( 1 - r^4 )

Aplicando na integral:

= int_0^(2 pi) int_0^1 ( r^3 - r^7 ) d r . cos^2 ( theta ) . d theta

Resolvendo a integral:

int_0^1 ( r^3 - r^7 ) d r = (r^4)/(4) - (r^8)/(8)

Aplicando o intervalo:

= (1^4)/(4) - (1^8)/(8) = (1)/(8)

Passo 3

Agora vamos colocar o resultado do passo 2 na equação:

= int_0^(2 pi) (1)/(8) cos^2 ( theta ) . d theta

= (1)/(8) int_0^((pi)/(2)) cos^2 ( theta ) . d theta

Lembrando que:

cos^2 ( theta ) = (1 + cos ( 2 theta ))/(2)

Substituindo:

= (1)/(8) int_0^(2 pi) ( 1 + cos ( 2 theta ) ) . d theta

= (1)/(16) [theta + int_0^(2 pi) cos (2 theta) . d theta]

Mais uma substituição aqui:

= (1)/(16) [theta + (1)/(2) s e n ( 2 theta )]

Aplicando o intervalo:

= (1)/(16) [2 pi + (1)/(2) [s e n (4 pi) - s e n (0)]]

= (1)/(16) [2 pi]

= (pi)/(8)

Prontinhoo!!

Resposta

(pi)/(8)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Região delimitada por paraboloides Encontre o volume daregião delimitada superiormente pelo paraboloide z = 5 – x2 – y2e inferiormente pelo paraboloide z = 4x2 + 4y2.
Encontre os volumes dos sólidos nos Exercícios 43-48.
Cilindro e planos Encontre o volume da região delimitadapelo cilindro x2 + y2 = 4 e os planos z = 0 e y + z = 4.
Esfera e cilindro Encontre o volume da região que está dentro da esfera x2 + y2 + z2 = 2 e fora do cilindro x2 + y2 = 1.
Esfera e paraboloide Encontre o volume da região delimitada acima pela esfera x2 + y2 + z2 = 2 e abaixo pelo paraboloide z = x2 + y2.