Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 3.16 - Ex. 28a
Calcular das funções dadas. Em seguida, conferir graficamente os resultados encontrados.
Passo 1
Esse é um limite que quando você vê, tem que lembrar que ele é daquele tipo de limites que dá alguma forma do , aquele número neperiano. Olha só a manipulação que vou fazer pra chegar nele. Lembrando que o limite que dá é esse aqui:
Passo 2
O nosso limite é esse aqui:
Ele já tá com bastante cara do limite que a gente queria, precisamos dar só uma ajeitadinha. Como a gente tá mexendo com o infinito, aquele do expoente é desprezível perto do , né? Fica assim então:
Pronto, já deu direto o que a gente queria, o próprio .
Passo 3
Traçando o gráfico, a gente vê que a função se aproxima de uma reta no infinito.
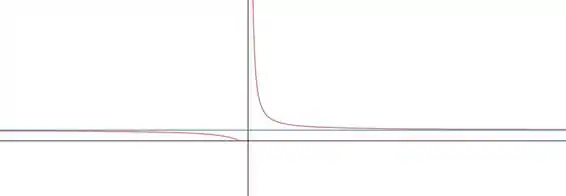
Essa reta é a própria . Sabemos disso porque foi a reta que eu botei pro programa fazer o gráfico, e bateu certinho! hahahah