Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 3.16 - Ex. 28b
Calcular das funções dadas. Em seguida conferir graficamente os resultados encontrados.
Passo 1
Vamos lá, primeiro vamos analisar o limite:
Ele parece muito com o limite fundamental exponencial:
Vamos então manipular um pouco a expressão do limite para tentar chegar a esse limite fundamental, vamos dividir o numerador e o denominador de por :
Agora vamos multiplicar e dividir por o expoente :
Pronto, chegamos ao limite fundamental exponencial, agora é só aplicar o valor dele:
Passo 2
Vamos conferir graficamente o resultado que achamos, dá pra ver no gráfico que quando vai pra a função tende a .
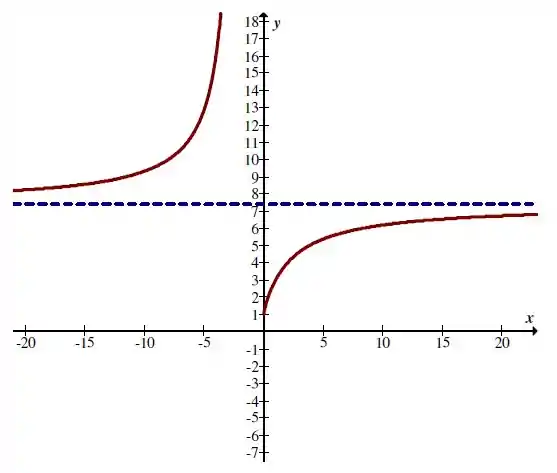
Então tá tudo certo!!
Resposta
Exercícios de Livros Relacionados
34. Encontre o limite ou demonstre que não existe. lim x → ∞ e 3 x - e - 3 x e 3 x + e - 3 x
33. Encontre o limite ou demonstre que não existe. lim x → ∞ a r c t g e x
41. Encontre as assíntotas horizontais e verticais de cada curva. Confira seu trabalho por meio de um gráfico da curva e das estimativas das assíntotas. y = 2 x + 1 x - 2
45. Encontre as assíntotas horizontais e verticais de cada curva. Confira seu trabalho por meio de um gráfico da curva e das estimativas das assíntotas. y = x 3 - x x 2 - 6 x + 5
36. Encontre o limite ou demonstre que não existe. lim x → ∞ s e n 2 ( x ) x 2 + 1