Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 35

Considere uma lâmina que ocupa, no primeiro quadrante, a região D limitada pela parábola x = 1 - y 2 e pelos eixos coordenados, com função densidade �� x , y = y .

a Determine a massa da lâmina.

( b ) Determine o centro de massa.

c Determine os momentos de inércia e os raios de giração em relação aos eixos x e y .

Passo 1

Opa, pessoal! Tudo tranquilo?

A questão tem 3 partes para resolvermos em relação a uma lâmina que ocupa, no primeiro quadrante, a região D limitada pela parábola

x = 1 - y 2

e pelos eixos x e y , com função densidade

ρ x , y = y

A parte (a) pede a massa da lâmina que é dada pela integral:

m = ∬ D ρ x , y d A

Então vamos precisar achar os limites de integração da região D e calcular a integral com:

d A = d x   d y  

A parte (b) pede o centro de massa dessa lâmina que é um ponto com coordenada:

x - , y -

Onde:

x - = M y m

y - = M x m

E o valor dessas coordenas a gente consegue calculando as seguintes integrais duplas:

M y = ∫ ∫ D x ⋅ ρ x , y ⋅ d A

M x = ∫ ∫ D y ⋅ ρ x , y ⋅ d A

Onde m é massa que vamos ter encontrado no passo 1. O processo é mesmo que usaremos para a parte (a).

Por último, temos a parte (c) que pede os raios de giração x - - em relação ao eixo y   e y   - - em relação ao eixo x :

m x - - 2 = I y

E:

m y - - 2 = I x

E os momentos de inércia

I x = ∫ ∫ D y 2 ρ x , y ⋅ d A

E:

I y = ∫ ∫ D x 2 ρ x , y ⋅ d A

Daí é só calcularmos essas integrais com os limites de integração que já teremos achado na parte (a).

Vamos lá!

Passo 2

Vamos começar com a parte (a) encontrando nossos limites de integração. Nossa região D é:

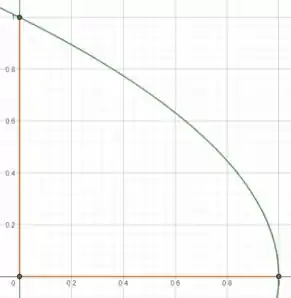
Parábola x = 1 - y 2 limitada pelos eixos x e y

Vamos escrever nossa região com uma região do Tipo I I , onde y está entre duas constantes e x está entre duas funções:

0 ≤ x ≤ 1 - y 2

0 ≤ y ≤ 1

Pronto, já temos os intervalos de integração para todas as integrais que vamos calcular nessa questão.

Agora já podemos escrever nossa integral da massa:

m = ∬ D ρ x , y d A

Como:

ρ x , y = y

E:

d A = d x   d y  

Ficamos com:

∫ 0 1 ∫ 0 1 - y 2 y   d x   d y

Passo 3

Vamos resolver essa integral, começando com a integral de dentro em x , tratando y como variável:

∫ 0 1 ∫ 0 1 - y 2 y   d x   d y = ∫ 0 1 x y 0 1 - y 2 d y

Aplicando os limites de integração:

= ∫ 0 1 1 - y 2 ⋅ y   d y = ∫ 0 1 y - y 3   d y

Agora ficou mais fácil do que já tava, né? Para resolver essa integral que ficou basta fazermos

∫ 0 1 y - y 3   d y = y 2 2 - y 4 4 0 1

Aplicando os limites:

= 1 2 - 1 4

Então nossa massa será:

m = 1 4

Passo 4

Para encontramos o centro de massa precisamos encontrar as coordenadas x   e   y dos mesmos.

x - = M y m

y - = M x m

Para isso, vamos precisar calcular as seguintes integrais:

M y = ∫ 0 1 ∫ 0 1 - y 2 x y   d x   d y   M x = ∫ 0 1 ∫ 0 1 - y 2 y 2   d x   d y    

Calculando cada uma das integrais teremos

M y = ∫ 0 1 ∫ 0 1 - y 2 x y   d x   d y  

Calculando a integram interna em x , tratando y como constante:

= ∫ 0 1 x 2 y 2 0 1 - y 2 d y  

Aplicando os limites de integração:

= ∫ 0 1 1 2 ⋅ y - y 2 d y

Integrando em y , temos:

M y = 1 2 ⋅ y 2 2 - y 3 3 0 1 = 1 12

Para a segunda integral vamos ter:

M x = ∫ 0 1 ∫ 0 1 - y 2 y 2   d x   d y  

Integrando primeiro em x , tratando y como constante:

= ∫ 0 1 x y 2 0 1 - y 2 d y

Aplicando os limites:

= ∫ 0 1 y 2 - y 4   d y

Assim, teremos a integral que resta:

M x = y 3 3 - y 5 5 0 1

Aplicando os limites:

M x = 1 3 - 1 5 = 2 15

Portanto, nosso centro de massa será x - , y - dado por:

x - = M y m = 1 12 1 4

y - = M x m = 2 15 1 4

Então:

x - , y - = 1 3 , 8 15

Passo 5

Por fim, para encontrarmos o momento de inércia total devemos calcular os momentos em x e y e somar ambos os valores.

I x = ∫ ∫ D y 2 ρ x , y ⋅ d A

E:

I y = ∫ ∫ D x 2 ρ x , y ⋅ d A

Para tal, temos que resolver então

I y = ∫ 0 1 ∫ 0 1 - y 2 x 2 y   d x   d y   I x = ∫ 0 1 ∫ 0 1 - y 2 y 3   d x   d y  

Para a primeira integral teremos

I y = ∫ 0 1 ∫ 0 1 - y 2 x 2 y   d x   d y  

Integrando em x , tratando y como constante e aplicando os limites de integração:

∫ 0 1 1 3 ⋅ y ⋅ 1 - y 2 3   d y =

Agora podemos integrar em y e aplicar seus limites:

- 1 24 ⋅ 1 - y 2 4 ​ 0 1 = 1 24

De igual maneira para a segunda integral teremos

I x = ∫ 0 1 ∫ 0 1 - y 2 y 3   d x   d y  

Integrando em x , e aplicando os limites de integração:

= ∫ 0 1 y 3 - y 5   d y

Agora integramos em y :

I y = 1 12

Para achar o momento de inércia total basta fazer

I t = I x + I y = 1 8

Agora, para achar os raios de giração devemos fazer o seguinte:

m x - - 2 = I y

E:

m y - - 2 = I x

Então:

y - - 2 = 1 12 1 4

Isolando y - - :

y - - = 1 3

De maneira análoga para x - - teremos:

x - - 2 = 1 24 1 4

Isolando x - - :

x - - = 1 6

Pronto, tá resolvido nosso problema.

Resposta

a 1 4

b x - , y - = 1 3 , 8 15

c   I x = 1 12 ,   I y = 1 24 , y - - = 1 3 , x - - = 1 6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcular o momento de inércia de um disco circular de diâmetro 10 cm:a) Em relação ao seu próprio centrob) em relação ao seu diâmetro Considerara densidade igual uma constante K
Uma lâmina ocupa a parte do disco x 2 + y 2 ≤ a 2 que está no primeiro quadrante. a Determine o centroide lâmina. ( b ) Determine o centro de massa da lâmina se a função densidade for ρ x , y = x y 2
Determine os momentos de inércia I x , I y , I 0 para a lâmina do Exercício 3 .
Centroide de um bumerangue Encontre o centroideda regiao em forma de bumerangue entre as parábolas y 2 = - 4 x - 1ey 2 = - 2 ( x - 2 ) no plano xy.