Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 10.11 - Ex. 26

Calcular

int int_S^() x (z^2 + y^2) d S

Onde S é o hemisfério da frente x ² + y ² + z ² = 9

Passo 1

Vamos considerar que “hemisfério da frente” seja a parte com fazemos projeção no plano YZ. Logo nossa região de integração vai depender de y e z. Vamos analisar nossa esfera

x^2 + y^2 + z^2 = 9

x = sqrt(9 - y^2 - z ²)

E nossa região vai ser

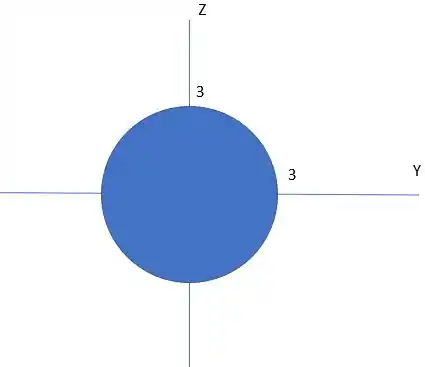
E também lembrar que nosso calculo vai ter essa forma

int int_S^() f d S = int int_R^() f (x ( y , z ) , y , z) sqrt(1 + ((del x)/(del y))^2 + ((del x)/(del z))^2) d y d z

Passo 2

Logo nossa integração fica

int int_R^() x (z^2 + y^2) sqrt(1 + ((d x)/(d y))^2 + ((d x)/(d z))^2) d y d z

Lembra que definimos uma expressão para x? então podemos usar essa expressão para substituir aqui

= int int_R^() sqrt(9 - y^2 - z ²) (z^2 + y^2) sqrt(1 + ((d x)/(d y))^2 + ((d x)/(d z))^2) d y d z

Passo 3

Vamos então calcular essas derivadas parciais

(d x)/(d y) = (d)/(d y) sqrt(9 - y^2 - z ²)

= - (2 y)/(2 sqrt(9 - y^2 - z^2)) -> - (y)/(sqrt(9 - y^2 - z ²))

O mesmo raciocínio vale para parcial em z

(d x)/(d z) = (d)/(d z) sqrt(9 - y^2 - z ²)

= - (z)/(sqrt(9 - y^2 - z ²))

Agora que chegou a parte de sermos sagazes. Nossa região de projetação é um circulo, talvez seria mais fácil Calcularmos essa integral em coordenadas polares. Vamos usar a seguinte equação então :

z^2 + y^2 = r^2

E também lembrar que estamos deformando o espaço. Em cartesiana, vemos o mundo em quadrados, já em polares vemos em círculos. Mudando de uma coordenada para a outra precisamos fazer uma correção pela distorção espaço – o Jacobiano. Nesse caso o Jacobiano de polar é r

= int int_R^() sqrt(9 - r ²) (r ²) r sqrt(1 + ((d x)/(d y))^2 + ((d x)/(d z))^2) d r d theta

= int int_R^() sqrt(9 - r ²) (r ²) r sqrt(1 + (- (y)/(sqrt(9 - y^2 - z ²)))^2 + (- (z)/(sqrt(9 - y^2 - z ²)))^2) d r d theta

= int int_R^() sqrt(9 - r ²) (r ²) r sqrt(1 + (y^2 + z^2)/(9 - y^2 - z ²)) d r d theta

= int int_R^() sqrt(9 - r ²) (r ²) r sqrt(1 + (r^2)/(9 - r^2)) d r d theta

Ficou grande essa conta!. Mas calma que já ta acabando. Vamos inclusive facilitar cortar as raízes, percebe só

= int int_R^() sqrt(9 - r ²) (r ²) r sqrt((9 - r^2 + r^2)/(9 - r^2)) d r d theta

= int int_R^() sqrt(9 - r ²) (r ²) r sqrt((9)/(9 - r^2)) d r d theta

Agora sim podemos cortar os termos sqrt(9 - r ²)

= int int_R^() (sqrt(9 - r^2))/(sqrt(9 - r^2)) (r ²) r sqrt(9) d r d theta

= int int_R^() 3 (r ²) r d r d theta

= int int_R^() 3 r^3 d r d theta

Agora basta inserir os limites de integração

int_0^(2 pi) int_0^3 3 r^3 d r d theta

Como nossa função não depende de theta podemos integrar logo em relação a essa variável

2 pi int_0^3 3 r^3 d r

= 2 pi ((3)/(4) r^4|_0^3

= 2 pi [(3)/(4) 3^4]

= (3^5)/(2) pi

UFAAA!!!! Essa conta foi grande, mas depois que montamos a integração fica mais tranquilo. Porque é so exercício de braço. Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

int int_S^() x (z^2 + y^2) d S = (3^5)/(2) pi

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral de superfície. ∫ ∫ Sy 2d S S é a parte da esfera x 2 + y 2 + z 2 = 4 que está dentro do cilindro x 2 + y 2 = 1 e acima do plano x y .
Calcule a integral de superfície. ∫ ∫ Syd S S é a parte do paraboloide y = x 2 + z 2 que está dentro do cilindro x 2 + z 2 = 4
Calcule a integral de superfície. ∫ ∫ Sx zd S S é a fronteira da região delimitada pelo cilindro y 2 + z 2 = 9 e pelos planos x = 0 e x + y = 5
Determine a área da superfície.A parte da superfície z = 1 + 3 x + 2 y 2 que está acima do triangulo com vértices 0,0 , 0,1 e 2,1
Determine a área da superfície.A parte do paraboloide x = y 2 + z 2 que está dentro do cilindro y 2 + z 2 = 9