Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 7.6 - Ex. 15

15. Calcular ∬_R^() ( x + 1 ) d x d y , sendo R a região delimitada por |x| + |y| = 1 .

Passo 1

Temos que a representação gráfica é a seguinte:

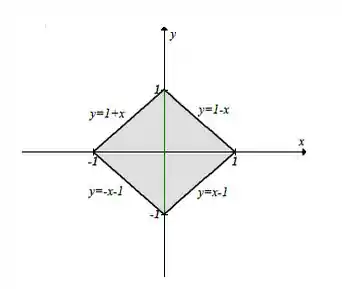
Seguindo a ordem de integração levando em consideração o gráfico, precisamos escrever duas integrais para obter a área desejada. Dessa forma, temos:

int_0^1 int_(y - 1)^(1 - y) ( x + 1 ) d x d y + int_(- 1)^0 int_(- y - 1)^(1 + y) ( x + 1 ) d x d y

Vamos integrar o primeiro termo e depois o segundo, para facilitar;

int_(y - 1)^(1 - y) ( x + 1 ) d x =

(((x^2)/(2) + x)|_(y - 1)^(1 - y) = ((1 - y)^2)/(2) + (1 - y) - ((y - 1)^2)/(2) - ( y - 1 )

Passo 2

int_0^1 (((1 - y)^2)/(2) + (1 - y) - ((y - 1)^2)/(2) - (y - 1)) d y =

((- (1)/(2) * ((1 - y)^3)/(3) - ((1 - y)^2)/(2) - (1)/(2) * ((y - 1)^3)/(3) - ((y - 1)^2)/(2))|_0^1 =

(1)/(6) + (1)/(2) - (1)/(6) + (1)/(2) = 1

Passo 3

Agora vamos resolver o segundo termo:

int_(- 1)^0 int_(- y - 1)^(1 + y) ( x + 1 ) d x d y

Primeiro vamos integrar em relação a x e depois em relação a y .

int_(- y - 1)^(1 + y) ( x + 1 ) d x =

(((x + 1)^2)/(2)|_(- y - 1)^(1 + y) = ((1 + y + 1)^2)/(2) - ((- y - 1 + 1)^2)/(2) =

((y + 2)^2)/(2) - ((- y)^2)/(2) = ((y + 2)^2)/(2) - (y^2)/(2)

Passo 4

int_(- 1)^0 (((y + 2)^2)/(2) - (y^2)/(2)) d y =

(((1)/(2) * ((y + 2)^3)/(3) - (1)/(2) * (y^3)/(3))|_(- 1)^0 =

(4)/(3) - (1)/(6) - (1)/(6) =

(4)/(3) - (2)/(6) =

(8)/(6) - (2)/(6) = (6)/(6)

= 1

Resposta final: 1 + 1 = 2

Resposta

2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule int int_B y d x d y onde B é o conjunto dado.
Calcule int int_B y d x d y onde B é o conjunto dado.
Calcule int int_B y d x d y onde B é o conjunto dado.
Calcule int int_B y d x d y onde B é o conjunto dado.
Calcule int int_B y d x d y onde B é o conjunto dado.