Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 3.1 - Ex. 5f
Calcule onde é o conjunto dado.
Passo 1
Chamando a integral dupla do teorema de Fubini de :
Ou:
E fazendo o desenho do conjunto :
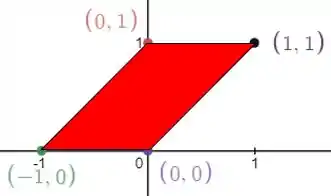
Pode-se observar que como a figura é um paralelogramo regular, a parte que está do lado negativo do eixo vertical pode completar o “vazio” que existe abaixo da parte que está do lado positivo desse mesmo eixo e, assim, forma um quadrado regular:
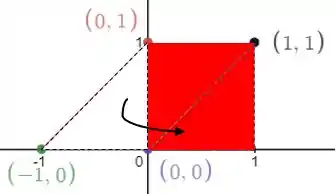
Como os lados horizontais e verticais da figura independem entre si, já que variam de a , pode-se calcular a integral diretamente.
Passo 2
Assim, é possível calcular para a primeira região:
Substituindo o intervalo de integração em :
Passo 3
Agora, integrando em relação a :
E, substituindo o intervalo de integração:
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 1-12, esboce a região delimitada pelas retas e curvas dadas. Em seguida, expresse a área da região como uma integral dupla iterada e calcule a integral. ap a r a b o l ax = y - y 2ear e
As integrais e somas de integrais nos Exercícios 13-18 fornecem as áreas das regiões no plano xy. Esboce cada região, marque cada curva limitante com sua equação e forneça as coordenadas dos pontos on
Nos Exercícios 1-12, esboce a região delimitada pelas retas e curvas dadas. Em seguida, expresse a área da região como uma integral dupla iterada e calcule a integral. ac u r v ay = e xea sr e t a sy
Nos Exercícios 1-12, esboce a região delimitada pelas retas e curvas dadas. Em seguida, expresse a área da região como uma integral dupla iterada e calcule a integral. a sp a r á b o l a sx = y 2ex =
Encontre o valor médio de ƒ(x, y) = s e n( x+y ) sobre: o retângulo 0≤x≤ π ,0≤y≤ π b) o retângulo 0≤x≤ π ,0≤y≤ π 2 .