Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 9.4 - Ex. 6
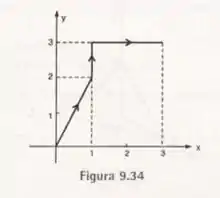
Calcular o trabalho realizado pela força sobre uma partícula ao longo de , que é mostrado na Figura 9.34.
Passo 1
Vamos lá, trabalho a gente calcula usando a integral:
Onde é a força e é o caminho parametrizado.
Aqui a força é e o caminho está dividido em três retas, que a gente vai ter que parametrizar cada uma.
Vamos calcular o trabalho realizado em cada reta e depois nós somamos as três.
Passo 2
Vamos para a primeira reta, que vai do ponto ao ponto . Uma equação paramétrica para ela é:
A derivada aqui é e aí calculamos o trabalho assim:
Passo 3
Vamos para a segunda reta agora, que vai de .
Uma equação paramétrica pra ela é:
A derivada é e o trabalho é:
Passo 4
A terceira reta vai de . Podemos parametrizar como:
Derivamos e encontramos:
Montamos a integral do trabalho agora:
Passo 5
Beleza, agora é só a gente somar os três trabalhos encontrados...
Prontinho! Esse é o trabalho😉