Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 7.10 - Ex. 14

Calcular o volume do sólido com uma base triangular no plano x y de vértices O 0 ,   0 ,   A ( 1 ,   1 ) e B ( 0 ,   2 ) , limitado superiormente por z = 2 x e lateralmente pelo contorno da base dada.

Passo 1

O sólido é delimitado superiormente por z = 2 x e inferiormente por z = 0 .

Desse modo, temos no plano x y :

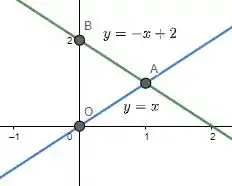
Passo 2

Temos o volume como:

V = ∬ 2 x d y d x

Sendo que:

x ≤ y ≤ - x + 2

0 ≤ x ≤ 1

Então:

V = ∫ 0 1 ∫ x - x + 2 2 x d y d x

Passo 3

Integrando para y :

∫ x - x + 2 2 x d y = 2 x y

Aplicando os limites:

- x + 2 - x ⋅ 2 x = - 4 x 2 + 4 x

Passo 4

Integrando para x :

∫ 0 1 ( - 4 x 2 + 4 x ) d x = - 4 3 x 3 + 2 x 2

Aplicando os limites:

1 - 0 ⋅ - 4 3 + 1 - 0 ⋅ 2 = 2 - 4 3 = 2 3

Resposta

2 3   u . v .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a área da superfície.
Encontre a área da superfície com precisão de quatro casas decimais expressado a área em termos de uma integral simples e usando uma calculadora para estimar a integral.
Encontre a área da superfície.
Encontre a área da superfície.
Encontre a área da superfície.