Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 6.4 - Ex. 6
Calcule onde é a curva do Exercício 5.
Passo 1
A curva em questão é dada pela imagem a baixo que criamos no software Geogebra
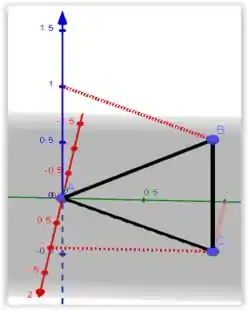
O Sentido que devemos adotar é o anti-horário, ou seja,
Passo 2
Vamos fazer por partes, no caso, 3 partes. Assim
Para
Com
Para
Com
Para
Com
Passo 3
Assim teremos que
Que nos dá
Onde a resposta do livro está errada, então tomer cuidado.
Resposta
Exercícios de Livros Relacionados
(a) Determine o trabalho realizado pelo campo de força F x ,y = x 2i + x yj sobre uma partícula que dá uma volta no círculo x 2 + y 2 = 4 no sentido anti-horário.(b) Utilize um sistema de computação a
Use um gráfico do campo vetorial F e a curva C para dizer se a integral de linha de F ao longo de C é positiva, negativa ou nula. Em seguida, calcule a integral. F x ,y = x - yi + x yj , C é o arco de
Use um gráfico do campo vetorial F e a curva C para dizer se a integral de linha de F ao longo de C é positiva, negativa ou nula. Em seguida, calcule a integral. F x ,y = x x 2 + y 2i + y x 2 + y 2j C
Mostre que um campo de força constante realiza trabalho nulo sobre uma partícula que dá uma única volta completa uniformemente na circunferência x 2 + y 2 = 1 .Isso também é verdadeiro para um campo d
Um objeto se move sobre a curva C , mostrada na figura abaixo, de ( 1,2 ) a ( 9,8 ) . Os comprimentos dos vetores do campo de força F → são medidos em newtons pela escala nos eixos. Estime o trabalho